

Sean Dunn
Presented on 2/17/1999
CS563
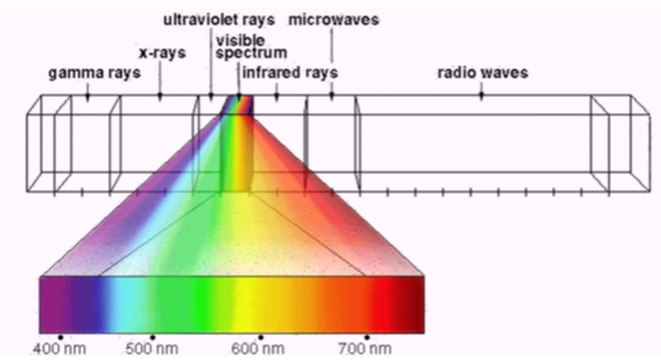
Radiant energy sends out waves. The many kinds of radiant energy create waves of varying frequencies, or lengths. Short waves can be smaller than a billionth of a meter. Very long waves, like radio waves, can be as long as a kilometer. The range of these waves is called the electromagnetic energy spectrum.

The human eye cannot see all radiant energy waves, such as radio waves, for example. The small range of frequencies that we can see is called the visible spectrum. Waves of light are measured in wavelengths, the length determining its color. Wavelengths of visible light range from 380nm to 760nm.
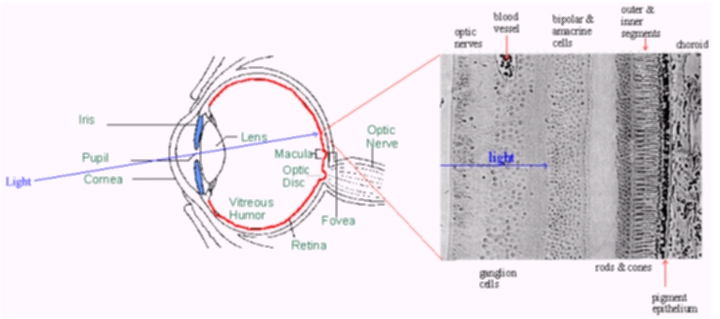
When light passes into the eye, the iris regulates the amount of light that flows through the lens to the retina. The lens focuses the light onto the retina.The retina, considered to be part of the brain, is a complex nerve structure containing receptors that are light-sensitive, and are responsible for translating incoming light into electrochemical nerve impulses. Because of how they are shaped, these receptors are know as rods and cones.
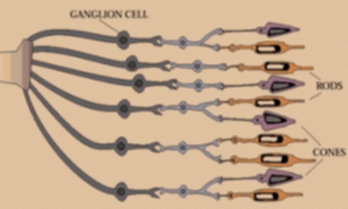
Rods Rods function in low or dim light and are responsible for night or low light vision. The rods in the retina are sensitive to a broad range of light intensities but do not distinguish color.
Cones Cones function in daylight and contain photo pigments, which are light-sensitive chemicals. These photo pigments contribute to the sensation of color. The cones are sensitive to different wavelengths, which the brain interprets as color. These wavelength, in their pure form, represent the colors red, green, and blue.
Optic Nerve The information from the rods and cones travels from the retina along the optic nerve to the brain. If some of the rods and cones are defective, the viewer's interpretation of some colors will be affected, and color blindness may result. Some individuals are born with these color vision abnormalities.
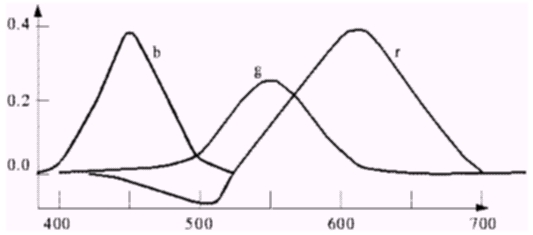
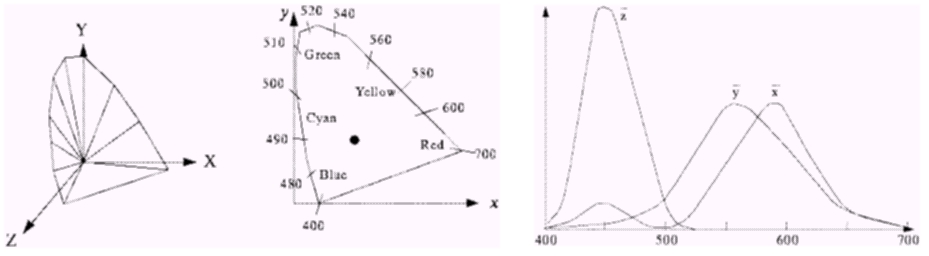
Most colors can be recreated using combinations of pure red, green, and blue. This graph shows the relative amounts of these primaries to recreate the colors of the visible spectrum.The negative values of red exist because not ALL colors in the visible spectrum can be created using positive amounts of red, green, and blue.
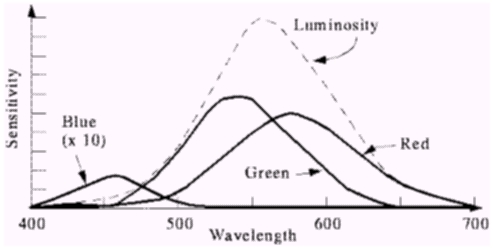
This graph shows the spectral response functions of the red, blue, and green cones in the eye, and the luminous efficiency function of the eye at those colors.
There exist many models through which to define the valid colors in image data. Each of the following models is specified by a vector of values, each component of that vector being valid on a specified range. This presentation will cover the following major color spaces definitions:RGB
CMY(K)
CIE XYZ
CIE L*a*b*
HLS (HSB, HSV)
YUV
YCrCb
YIQ
RGB is perhaps the simplest color space for us to understand. As stated above, using proportions of red, green, and blue that are scaled to a minimum and maximum values for each component (for example, 0x00 through 0xFF, or 0.0 through 1.0), most colors in the visible spectrum can be recreated, although not completely. This scheme is based on the additive properties of color.

CMY (cyan, magenta, yellow) is the basic color space used when applying colors to media printed on a white background (such as paper). It is based on the subtractive properties of color, which is caused by wavelength absorption. For example, the color yellow appears yellow because yellow objects absorb blue, and reflect red and green.When CMY colors are added, the subtractive properties are compounded. An example of this would be obtaining the color blue in CMY space. You basically want to absorb everything but blue (red and green). Green and red are absorbed by cyan and magenta, respectively. The resulting vector becomes <1,1,0>.
The ideal general equation (with normalized vector components) for translating between CMY and RGB is the following:
C = 1 - R
M = 1 - G
Y = 1 - B
There is also a very closely related color space known as CMYK, for which there exists the fourth component K, which is pure black. This color space is useful in printing, where K can be mixed into the CMY inks to produce a much darker black than could be produced by saturating the paper with ridiculous amounts of cyan, magenta, and yellow. The mixing function is:
K = minimum(C,M,Y)
C = C - K
M = M - K
Y = Y - K
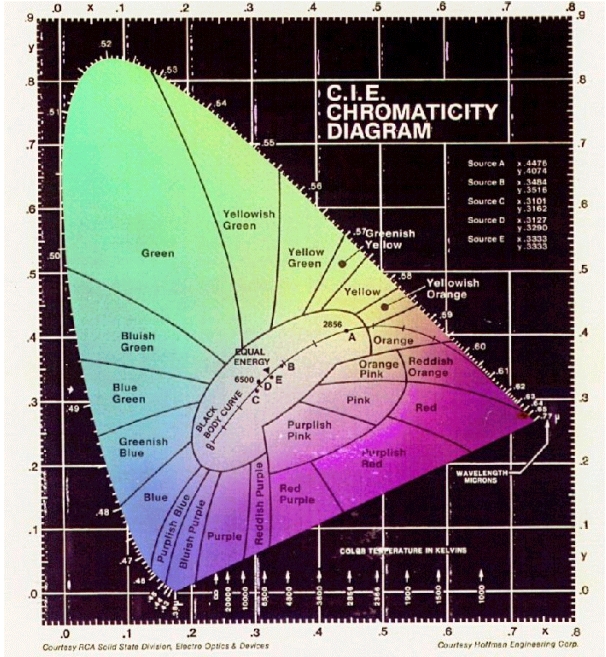
CIE (Commission Internationale de L'Eclairage) XYZ is a complete model developed in 1931 that can recreate all colors in the visible spectrum. XYZ defines virtual primarycolors X, Y, and Z, which are the wavelengths that the rods and cones in the human eye are most sensitive to. The Y primary was specifically designed to follow the luminous efficiency function of human eyes.
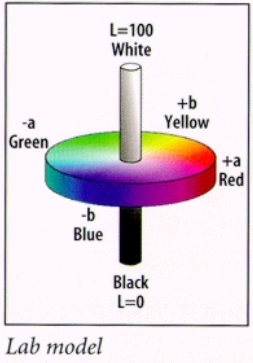
In 1976 the CIE created a refined model of XYZ called L*a*b*. In L*a*b*, L is the luminance, a* is a value for which -a* is green, and +a* is red, b* is a value for which -b* is blue, and +b* is yellow.Use the following formular to convert from CIE XYZ to CIE L*a*b*:
L* = -16 + 116 * (pow(Y / Yn), 1/3)
a* = 500 * (pow(X / Xn, 1/3) - pow(Y / Yn, 1/3)
b* = 200 * (pow(Y / Yn, 1/3) - pow(Z / Zn, 1/3)
where X,Y,Z exist on the scale of 0,0,0 to Xn,Yn,Zn.
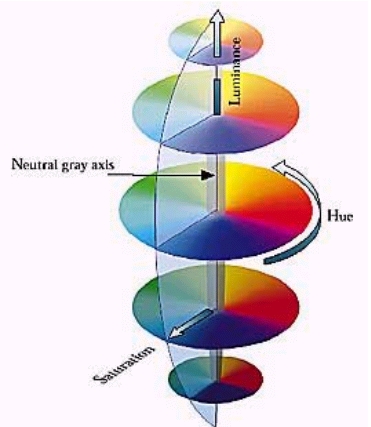
HLS stands for hue, lightness (luminence), and saturation.Luminence is the brightness of the color - the intensity.
Hue is the shift in the dominant wavelength of a spectral distribution.
Saturation is the concentration of a spectral distribution at one wavelength.
HLS is in the same class of color spaces as HSB, and HSV. The brightness computation is the only difference.
Originally used for PAL (European "standard") analog video, YUV is based on the CIE Y primary, and also chrominance. Chrominance is the difference between a color and a reference white at the same luminance.To convert from RGB to YUV spaces, the following equations can be used:
Y = 0.299 R + 0.587 G + 0.114 B
U = 0.492 (B - Y)
V = 0.877 (R - Y)

YCrCb is a subset of YUV that scales and shifts the chrominance values into the range of 0..1:Y = 0.299 R + 0.587 G + 0.114 B
Cr = ((B-Y)/2) + 0.5
Cb = ((R-Y)/1.6) + 0.5
YIQ is used in the US television standard, NTSC. It is similar to YUV, except that its colorspace is rotated 33 degrees clockwise, so that I is the orange-blue axis, and Q is the purple-green axis. The equations to convert from RGB to YIQ are:Y = 0.299 R + 0.587 G + 0.114 B
I = 0.74 (R - Y) - 0.27 (B - Y) = 0.596 R - 0.275 G - 0.321 B
Q = 0.48 (R - Y) + 0.41 (B - Y) = 0.212 R - 0.523 G + 0.311 B
[1] Pirazzi, C., "The Pixel Rosetta Stone: Packings and Colorspaces,"
http://reality.sgi.com/cpirazzi_engr/lg/packings/index.html[2] Li, Ze-Nian, "CMPT 365 Multimedia Systems '98,"
http://www.cs.sfu.ca/CourseCentral/365/li/