Hierarchical Structure

Explicit: use partitions of a single dimension to define layer of tree

Implicit: use clustering algorithms which combine influences of dimensions

Goal is to find placement algorithms which best convey structure

May use additional graphics (e.g., edges) to convey relationships

Node-link graphs vary by

• where the root node is relative to the rest of the tree (e.g., centered, top-most)
• relative direction between a node and its children (e.g., radially outward, horizontal, vertical, or alternating horizontal and vertical).
• 2-D or 3-D (as in Cone Trees [41] and Disc Trees [23]).
• Augment node-link graphs with glyphs, use aggregations for non-terminal nodes

Filled-region graphs convey structure with position

• Tree-maps recursively divide display space based on subtree population
• Alternate horizontal and vertical slices
• Result mostly univariate (colored box)
• Some relationship to dimensional stacking and N-land
• Glyph variant not space-filling, unless using deformable glyph

  

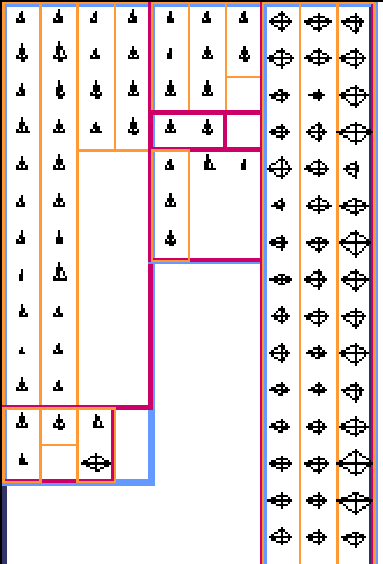
Figure: Star glyphs of Iris data set using recursive hierarchical placement based on the DySect [2] data partitioning algorithm and the Tree-map [24] recursive space partioning technique.