Present for CS563 on 3/31/99
Tom Germano
Present for CS563 on 3/31/99
Tom Germano
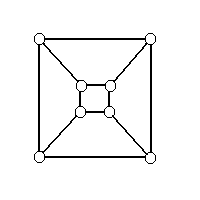
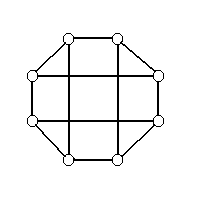
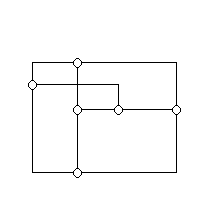
The problem that graph drawing tries to tackle is how to represent a set of edges and vertices in such a way that it will convey the most meaning. There are many ways to draw a single graph and each graph will draw to attention different connections and relations between vertices. For example, the following two pictures are the same graphs but show different properties of the graph:
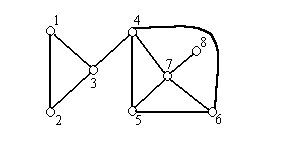
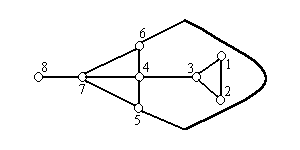
Looking at the graph on the right, it is very hard to see that vertex 4 has so many connections and it is hard to tell that vertex 3 and 7 only have one vertex separating them and are therefor relatively close.
As you can see, even though they are mathematically the same exact graph,
the drawings of the two convey different information. The goal of graph
drawing is to try to draw graphs in such a way that they convey the most
information possible.
V={1,2,3,4,5,6,7,8}
E={{1,2},{1,3},{2,3},{4,3},{4,5},{4,6},{4,7},{7,8}}
which can be represented visually with the following picture:

Each of the numbered points are the vertices and the black lines connecting them are edges.
Edges can also have direction which creates a directed graph, or di-graph. Some graphs also have graphs inside them called sub-graphs.
A bend is where a straight line changes direction and a jordan curve is a line that does not cross over itself, the edge connecting 5 and 6 is a jordan curve.
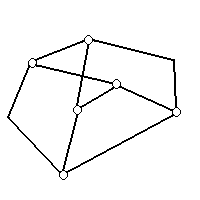
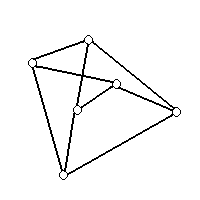
A planar graph drawing is a drawing in which none of the lines. The drawing on the left is a planar drawing, the drawing on the right is not.
Drawing conventions are restraints placed on drawing algorithms when creating the final drawing. For example one constraint does not allow bends in the final drawing while another allows bends, but only at right angles.
The polyline drawing means that the final drawing can have as many bends in the edges as desired.
What is it that makes a good graph good? How is it possible that one graph can be objectively better than another graph? The attributes that define a good graph are called aesthetics and were determined through statistical analysis in [BFN85], [PCJ96], and [STT81]. The qualities which they determined define a good graph are as follows:
Drawing constraints are constraints placed on the drawing algorithm in order to create the final drawing. There are two purposes to applying constraints when drawing a graph. The first advantage is that this gives the user the ability to pre-arrange certain shapes and allows more control the outcome of the drawing. Also, graph drawing can be a very computationally expensive operation. Applying constraints can greatly speed up the process. The constraints that can be placed on a graph drawing algorithm are as follows:
This graph drawing approach is a three tiered refinement of the initial graph. The resulting drawings of this approach are orthogonal which are often used for electrical engineering schematics along with other practical applications. This approach also stresses the minimization of crossings in the drawing because the first step in the procedure is planarization.
The three forms that a raph can take in this approach are topology, shape, and metric. Two graphs share the same topology if one can be made into the other using deformation while not disturbing the order of the vertices and edges. If two graph drawings share the same shape, then one can be made into the other by changing the lengths of the edges, but not the angles formed by the edges. The last refinement of the approach is a metric where two graphs share the same metric if one graph can be made into the other by using only translation and rotation.
The general procedure for the Topology Shape Metrics approach is that the graph first goes through the process of planarization. In this step, the graph is converted from its mathematical representation (in this case V={1, 2, 3, 4, 5, 6} and E={(1,4), (1,5), (1,6), (2,4), (2,5), (2,6), (3,4), (3,5), (3,6)} ) into a 2d drawing where the number of crossings are kept to a minimum. The process of planarization has been studied very carefully and Battista et al. refer the reader to [CNS79, JLM97, JM96, JTS86, Kan92b, NT84]. If there are any crossings in the planarized graph, they are replaced with dummy vertices. The output of this process is the first form, a topology.
Once the graph has been planarized, the graph is then orthogonalized. In this step the bends are made to go at right angles and the vertices are aligned. The result of this step is a shape.
The final step of this approach is called compaction. In this process, the dummy vertices are removed and the graph is made to take up a minimum amount of area. After this step, the final graph is a metric.
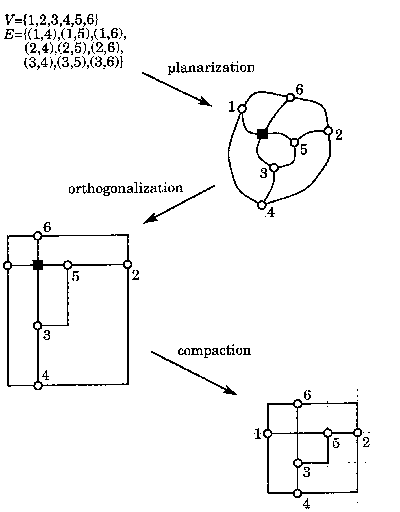
Di Battista, G. , Eades, P., Tamassia, R., Tollis, I., Graph Drawing: Algorithms for the Visualization of Graphs, Prentice Hall, Upper Saddle River, 1999, p. 21
The above picture is an example of the three steps in the topology
shape metrics paradigm. The first step is planarization and a crossing
is replaced with a dummy vertex. From this step, the graph is made into
an orthogonal drawing and then compacted into its final drawing.
The hierarchical approach is a way of making hierarchies from directed graphs. Hierarchies have numerous uses to them including class diagrams, and PERT charts.
The first step in the hierarchical approach is called layer assignment. In this step, the vertices are assigned layers which begin at the top and go down for a downward graph. Each vertex is assigned a layer Ln, such that if there is an edge from u to v, u and us layer is Li and vs layer is Lj, then i<j. If there is a gap in between layers, such as when there is an edge from L1 to L3, a dummy vertex is placed at L2.
Following the layer assignment, the graph drawing goes through a process called crossing reduction. Here, the amount of times that edge cross over is reduced to create a more aesthetically pleasing drawing.
The final step is called x-coordinate assignment. In this stage, all the points are assigned a position, the dummy vertices are removed, and the edges are all drawn. In this stage many different aesthetics can be stressed such as minimizing bends or minimizing area.
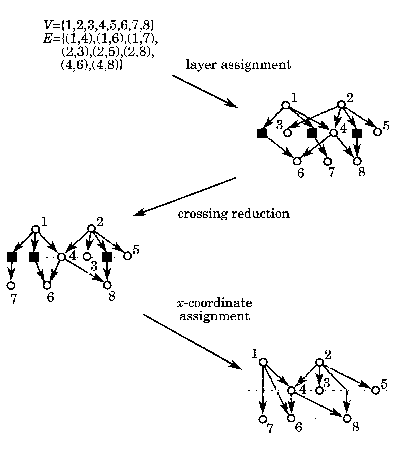
The above figure is an example of the hierarchical paradigm in process.
The layers are assigned and dummy vertices inserted. Next the number of
times that lines cross are reduced and then the final drawing is made without
the dummy vertices.
The visibility approach to graph drawing is an all-round general purpose polyline drawing technique. As in the topology shape metrics approach, the first step in the visibility paradigm is planarization. Again, having this process as the first step places a high priority on the reduction of crossings.
The visibility step in this paradigm is hard to explain without looking at the figure below. Basically, each vertex is changed into a horizontal bar including the dummy vertex. All the edges are then replaced with vertical bars connecting the horizontal bars.
A final drawing is then produced once the replacement step has been completed. In this step, the horizontal bars are replaced with single points and the edges are drawn so that they closely follow the vertical bars.
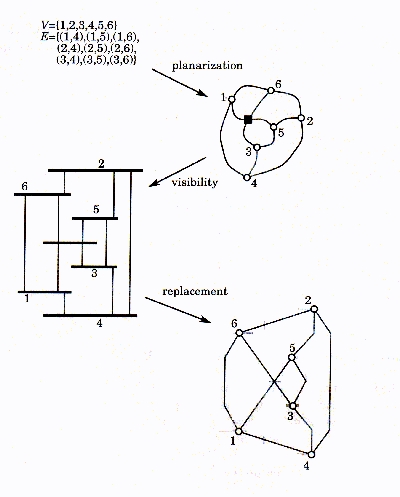
Di Battista, G. , Eades, P., Tamassia, R., Tollis, I.,
Graph Drawing:
Algorithms for the Visualization of Graphs, Prentice Hall, Upper Saddle
River, 1999, p. 26
As mentioned above, because planarization is the first step in this
paradigm, the minimizing of crosses takes a high priority. The aesthetic
of minimizing the area is stressed in the visibility stage and in the final
step a number of different aesthetics can be stressed depending on the
users preference.
The augmentation approach is similar to the visibility approach in that it is a general purpose graph drawing paradigm and its first step is planarization.
The second step is called the augmentation step. In this process, dummy edges are drawn in order to obtain a graph in which all the faces have three side (maximal planar.) In the example below you can see that in the first drawing, the face of {3,5,2,4} has four sides to it. Once the augmentation step is complete, a dummy edge {3,2} is drawn making two 3-sided faces, {3,5,2} and {3,2,4}.
In the triangulation step, the final graph is drawn by using geometric properties of the triangles formed in the previous step. The dummy vertices and edges are also removed in this step.
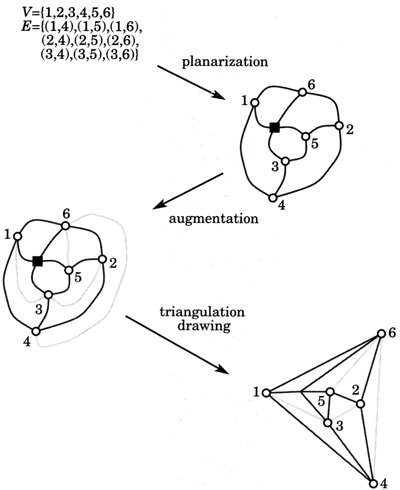
Di Battista, G. , Eades, P., Tamassia, R., Tollis, I., Graph Drawing: Algorithms for the Visualization of Graphs, Prentice Hall, Upper Saddle River, 1999, p.28
Again this paradigm stresses minimizing crossing, but in addition to
this aesthetic it also attempts to minimize bends because of the straight-line
approach to the triangulation. Had the above example been a planar graph,
the final drawing would have been straight line meaning no bends at all.
Force directed graphs are popular because they are very easy to understand and easy to code. In this paradigm, the graph is represented as a system of forces and the final graph produced is graph with the small energy configuration. There are two basic components to a force-directed graph:
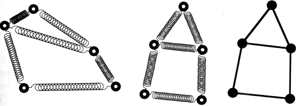
Di Battista, G. , Eades, P., Tamassia, R., Tollis, I., Graph Drawing: Algorithms for the Visualization of Graphs, Prentice Hall, Upper Saddle River, 1999, p. 303
The above figure is a three step process of what happens in a force-directed drawing procedure and the force model here are springs. The first frame is not at a very low energy because in the second frame the drawing is more settled. In the final frame, the graph drawing for the force model is shown.
Drawings produced with this paradigm are often very symmetrical. An
added advantage to the force directed paradigm is that if you want a
particular vertex to be far from another particular vertex, all you need
to do is increase the force on the edge connecting them and the two will
stay away from each other.
This approach is basically what the names says, the graph is divided
into smaller subgraphs which are then easily drawn. Then the graphs are
all combined to form the final drawing. There are many different techniques
to the divide and conquer method where different aesthetics can be stressed.
[BFN85]
C. Batini, L. Furlani and E. Nardelli, What is a Good Diagram? A
Pragmatic Approach, In Proc. 4th Internat. Conf. on the
Entity Relationship Approach, 1985.
[CNS79]
N. Chiba, I. Nishioka, and I. Shirakawa, An Algorithm of Maximal
Planarization of Graphs, In Proc. IEEE Internat. Sympos. on Circuits
and Systems, pp. 649-652, 1979.
[JLM97]
M. Jünger, S. Leiper, and P. Mutzel, Pitfalls of using PQ-trees
in automatic graph drawing, In G. Di Battista, editor, Graph Drawing
(Proc. GD 97), vol. 1353 of Lecture Notes in Computer Science,
pp. 193-204. Springer-Verlag, 1997.
[JM96]
M. Jünger and P. Mutzel, Maximum Planar Subgraphs and Nice
Embeddings: Practical Layout Tools, Algorithmica, 16, 33-59, 1996,
(special issue on Graph Drawing, edited by G. Di Battista and R. Tamassia).
[JTS86]
R. Jayakumar, K. Thulasiraman, and M. N. S. Swamy, An Optimal Algorithm
for Maximal Planarization of Nonplanar Graphs, In. Proc. IEEE Sympos.
on Circuits and Systems, pp. 1237-1240, 1986.
[Kan92b]
G. Kant, An O(n2) Maximal Planarization Algorithm based
on PQ-trees, Technical Report RUU-CS-92-03, Dept. Comput. Sci., Utrecht
Univ., Utrecht, Netherlands, 1992.
[NT84]
E. Nardelli and M. Talamo, A Fast Algorithm for Planarization of
Sparse Diagrams, Technical Report R. 105, IASI-CNIR, Rome, 1984.
[PCJ96]
H. C. Purchase, R. F. Cohen and M. James, Validating Graph Drawing
Aesthetics, In F. J. Brandenburg, editor, Graph Drawing (Proc
GD 95), vol. 1027 of Lecture Notes Comput. Sci., pp. 435-446. Springer-Verlag,
1996.
[STT81]
K. Sugiyama, S. Tagawa and M. Toda, Methods for Visual Understanding
of Hierarchial System, IEEE Trans. Syst. Man Cybern., SMC-11, no. 2,
109-125, 1981.
Di Battista, G. , Eades, P., Tamassia, R., Tollis, I., Graph Drawing: Algorithms for the Visualization of Graphs, Prentice Hall, Upper Saddle River, 1999.
Trudeau, R., Dots and Lines, Kent State University Press, 1976.
Preparata, F., Shamos, M., Computational Geometry: An Introduction, Springer-Verlag, New York, 1985.
Thulasirama, K., Swamy, M., Graphs: Theory and Algorithms, John
Wiley and Sons, New York, 1992.