Wavelets in Multiresolution Analysis

Presented 2/15/99 for CS563
by Tom Germano


Table of Contents

  1. Introduction
  2. Linear Algebra Review
  3. Concepts of Multiresolution Analysis
  4. The Haar Wavelet
  5. Haar Wavelet Example
  6. Filter Banks
  7. Image Thresholding
  8. References
    1. Books
    2. Papers
    3. Web Pages
  9. Links

Introduction

In signal analysis, there are a number of different functions one can perform on that signal in order to translate it into different forms that are more suitable for different applications. The most popular function is the Fourier transform that converts a signal from time versus amplitude to frequency versus amplitude. This transform is useful for many applications, but it is not based in time. To combat this problem, mathematicians came up with the short term Fourier transform which can convert a signal to frequency versus time. Unfortunately, this transform also has its shortcomings mostly that it cannot get decent resolutions for both high and low frequencies at the same time.

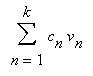
So how can a signal be converted and manipulated while keeping resolution across the entire signal and still be based in time? This is where wavelets come into play. Wavelets are finite windows through which the signal can be viewed. In order to move the window about the length of the signal, the wavelets can be translated about time in addition to being compressed and widened.
 
 

Linear Algebra Review

Unfortunately in order to understand the wavelets, you must understand linear algebra because wavelets make use of vector spaces and matrices quite a lot. Matrices are pretty straight forward and all their functions are covered by using Maple so I won’t bother going over them, instead below I have written a brief introduction to the terms and functions of vectors spaces.

Basically a vector space is a set of vectors such as V=[(0,1),(1,0),(1/2,1/2),(-1/2,0)]. In addition to defining a vector space by explicitly stating all the vectors that make up the space, you can also define a vector space using a function. When reading material on wavelets, the vector space L2 is often mentioned meaning the 2 dimensional plane of real numbers. This vector space can be thought of as the plane made up by the x and y axis. There are three important terms to learn for understand vector spaces and these terms of often used in discussions of wavelets with respect to their use in multiresolution analysis.

Linear combination – this is the easiest term to understand. It is simply the sum of a set of vectors or equations where each vector, value, or function is multiplied by some real constant. It is represented mathematically by the following:

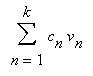
Span – a span is a set of vectors whose linear combination can create all of the other vectors in the vector space. For example, using i=(1,0) and j=(0,1) we can recreate any of the vectors mentioned above through a linear combination.

i*1 + j*0 = (0,1)
i*0 + j*1 = (1,0)
i*(1/2) + j*(1/2) = (1/2,1/2)
i*(-1/2) + j*0 = (-1/2,0)

So we can say that the vectors [(1,0),(0,1)] span the vector space V mentioned above. If we try to see if just the vectors i=(1,0) and k=(-1/2,0) span V, we’ll see that it does not work.

i*1 + k*0 = (1,0)
i*(-1/2) + k*0 = (-1/2,0)

That works fine, but no matter how hard you try you will never make (0,1) using just I and k, so we can say that the vectors i and k do not span vector space V.

Basis – This is the smallest set of vectors that can span a vector space. If we create a sub set of our vector space V called S consisting of the set [i,j,k], we can say that it spans V, but is not a basis for V. Why, because we can eliminate k from S since k can be created using i and j. So, S is not a basis, but a set of the vectors [i,j] is a basis for vector space V. This is not the only basis for V, another basis could be the vector (1/2,1/2) and (-1/2,0), since those two can also create all the other vectors.
 
 

Concepts of Multiresolution Analysis

The first component to multiresolution analysis is vector spaces. For each vector space, there is another vector space of higher resolution until you get to the final image. Also, each vector space contains all vector spaces that are of lower resolution. The basis of each of these vector spaces is the scale function for the wavelet.

For practical purposes one can think of an image as a vector space such as Vj would be the perfectly normal image, and Vj-1 would be that image at a lower resolution until you get to V0 where you just have one pixel in the entire image. For each vector space Vj, there is an orthogonal complement called Wj and the basis function for this vector space is the wavelet.
 
 

The Haar Wavelet

Everyone starts with the haar wavelet because it’s so simple. The piecewise functions that make up the Haar wavelet and their graphs are as follows:

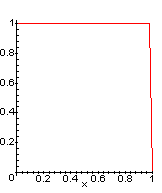
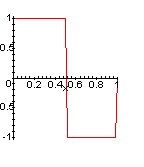
These are the root functions for the haar wavelet. fis what is called the scale of the haar wavelet, y is the actual wavelet. With these two functions alone, you really cannot do much, so you must create a function where you can translate and scale both of these functions which are the following:

i is responsible for the scaling of the function, it basically shrinks and expands the graph the function makes and represents the resolution of the function.

j is the translation of the graph across the time axis. Note how as the resolution increases, the number of possible translations increases exponentially.

Also, f(i,j) and y(i,j) for the haar wavelet do not call themselves unlike some other wavelets, they call the piecewise functions mentioned above. To show how these functions actually work, see the Animations section in this Maple worksheet.
 
 

Haar Example

So how are these functions actually used to do something such as compressing a signal? Well, the easiest way is to show first using a very simple example. Given four points of data, say values of a pixel in an image, the haar wavelet can be used to compress this data through a process called averaging and differencing.

Pixel Values
[9 7 3 5]   (9+7)/2 = 8
            (9-7)/2 = 1
            (3+5)/2 = 4
            (3-5)/2 = -1

[8 4 1 –1]  (8+4)/2 = 6
            (8-4)/2 = 2

[6 2 1 –1]

There are two types of data here, the sparse data and the detailed data. The sparse data is what we want to get rid of and in this examples are the numbers [9,7,3,5,8,4,6]. The other data type here are the details which make up the differences when doing our compression and here they are [2,1,-1].

This may look wonderful and all, but what good is compression that takes four values and compresses it to four values? Simple, in images especially, the pixel values are similar to their neighbors. If they weren’t we would be looking at random static and there would not be an object. When doing the averaging and differencing with wavelets, the detail values are usually low numbers and sometimes zero. These detail values (which compose all but one of the resulting values) can be compressed much better than the original pixel values. In this example, the number [6 2 1 –1] are more easily compressible than [9 7 3 5].
 
 

Filter Banks

As mentioned in the haar wavelet example, there are two kinds of data: the sparse data and the detailed data. These coefficients are extracted from the original set of number by using two kinds of filters, high pass (details) and low pass (average.) The two filters are applied, the filtered data from the high pass filter is stored as coefficients for later reconstruction of the signal. The filtered data from the low pass filter is now treated as the original data and the low and high pass filters are then applied to this data. This is repeated until the filtered data from the low pass filter outputs only one number.

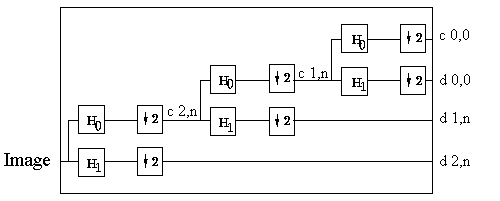
Here we see what happens to an array of 8 values. First the values are filtered with the high and low pass filters. The data from the high pass filter is stored and the data from the low pass filter is filtered again. This process repeats until there is only one value left and since the averaging and differencing works in pairs, that value is saved. For my examples, the differences are stored in an array called d and the coefficients of the actual values and sparse values are stored in an array called c. To see how these filter banks are applied using matrices, please review the Maple worksheet.
 
 

Image Thresholding

When compressing an image, as you progress down the resolution of the image to the single pixel, the importance of the detail coefficients increases. To account for this, some people multiply their equations by 2(j/2) where j again is the resolution, the scalar, of the wavelet. For example, if we have the set of numbers:

[1,0,-3,2,1,0,1,2]

We can do our normal compression and get the following:

[.5, -.5, .5, -.5, .5, -2.5, .5, -.5]

Or we can implement the scaling of 2(j/2) and get this:

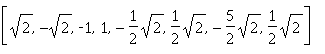
From here we can do a better job of applying a threshold on our detail values. In this example we can scale any value at or below 1/sqrt(2) to 0 and get the following as our new coefficients:

How well does this thresholding mangle our orginial data? Here are the plots of the original data and reconstructed data with the thresheld coefficients followed by the comparison of the two:

Why would anyone possibly want to do something like this to their data? Well, when dealing with a lot of points, there are sometime too many and may obscure important data. In this picture, there are so many points, that the middle line is hidden. To bring this middle line out, the data is compressed, any points below a certain threshold are set to zero, and the image on the right is the reconstructed line.


References

Books

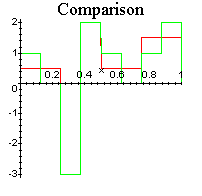
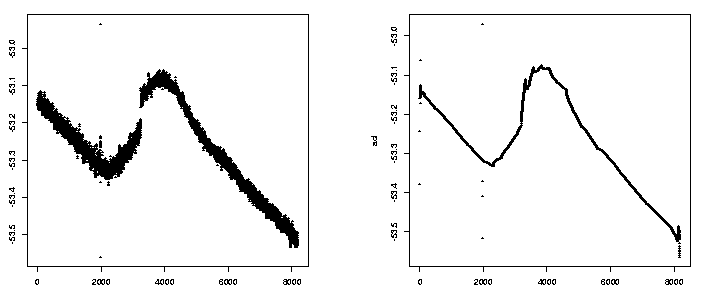
Chui, Charles K., An Introduction to Wavelets, Academic Press, Boston, 1992.

Chui, Charles K., Wavelets: A Tutorial in Theory and Applications, Academic Press, Boston, 1992.

Daubechies, Ingrid, Different perspectives on wavelets : American Mathematical Society Short Course, January 11-12, 1993, San Antonio, Texas.

Daubechies, Ingrid, Ten lectures on Wavelets, Society for Industrial and Applied Mathematics, Kolman,

Iyengar, S. S., Prasad, L., Wavelet Analysis wth Applications to Image Processing, CRC Press, Boca Raton, 1997.

Kolman, Bernard, Introductory Linear Algebra with Applications, Prentice Hall, New Jersey, 1997.

Renikoff, Howard L., Wells, Raymond O. Jr, Wavelet Analysis: The Scalable Structure of Information, Springer-Verlag, New York, 1998

Stuart, R. D., An Introduction to Fourier Analysis, Science Paperback, Cambridge, 1966.

Walter, Gilbert G., Wavelets and Other Orthogonal Systems with Applications, CRC Press, Boca Raton, 1994.
 

Papers

S. G. Mallat, "A Theory for Multiresolution Signal Decomposition: A Wavelet Representation," IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol 11, No. 7, July 1989.

E. J. Stollnitz, T. D. DeRose, D. H. Salesin, "Wavelets for Computer Graphics: A Primer Part I", IEEE Computer Graphics and Applications, 15, May 1995.

E. J. Stollnitz, T. D. DeRose, D. H. Salesin, "Wavelets for Computer Graphics: A Primer Part II", IEEE Computer Graphics
and Applications, 15, July 1995.

C. Mulcahy, "Image Compression Using the Haar Wavelet Transform,"

C. Mulcahy, "Plotting and Scheming with Wavelet," Mathematics Magazine 69, 5, 1996.

G. Strang, "Wavelets and Dilation Equations: A Brief Introduction," Siam Review 31, 1989.

P. Muller, B. Vidakovic, "Wavelets for Kids: A Tutorial Introduction," 1991.
 

Web Pages

B. Lipchak, "2D and 3D Progressive Transmission Using Wavelets," http://www.cs.wpi.edu/~matt/courses/cs563/talks/Wavelet_Presentation/Wavelet_Presentation.html

A. Nicolaou, "A Wavelet Wading Pool," http://www.cgl.uwaterloo.ca/~anicolao/wadingpool/WaveletWadingPool.html

R. Polikar, "The Wavelet Tutorial Part I: Fundamental Concepts and an Overview of the Wavelet Theory," http://www.public.iastate.edu/~rpolikar/WAVELETS/WTpart1.html

R. Polikar, "The Wavelet Tutorial Part II: Fundamentals: The Fourier Transform and the Short Term Fourier Transform," http://www.public.iastate.edu/~rpolikar/WAVELETS/WTpart2.html

R. Polikar, "The Wavelet Tutorial Part III: Multiresolution Analysis and the Continuous Wavelet Transform," http://www.public.iastate.edu/~rpolikar/WAVELETS/WTpart3.html

R. Polikar, "The Wavelet Tutorial Part IV: Multiresolution Analysis: The Discrete Wavelet Transform," http://www.public.iastate.edu/~rpolikar/WAVELETS/WTpart4.html

D. Zorin, J. Owens, "Introduction to Wavelets," http://www-graphics.stanford.edu/courses/cs448-97-fall/notes.html

D. Zorin, J. Owens, "Introduction to Wavelets II," http://www-graphics.stanford.edu/courses/cs448-97-fall/notes.html
 
 

Links

http://www.wavelet.org/wavelet/index.html – Wavelets newsletter

http://www.amara.com/current/wavelet.html – Amara’s Wavelets Page containing tutorials and many links

http://dir.yahoo.com/Science/Mathematics/Wavelets/ - Wavelets at Yahoo

http://www.mathsoft.com/wavelets.html – Huge resource of papers about wavelets

http://www.multires.caltech.edu/teaching/courses/waveletcourse/ - Wavelets in computer graphics

http://www.cs.washington.edu/research/projects/grail2/www/pub/abstracts.html – More papers on the applications of wavelets in computer graphics

http://cas.ensmp.fr/~chaplais/Wavetour_presentation/Wavetour_presentation_US.html – A Wavelet Tour of Signal Processing by Stephane Mallat

http://www-graphics.stanford.edu/courses/cs448-97-fall/notes.html – Stanford course with lecture notes on computer graphics
 


[Return to CS563 '99 talks list]