Smoothing

    The method we used was to change the control points. A simple method would be to skip a certain amount of given control points in the medial axis data, but this would be a waste of data. A better alternative to this idea is to take an average of the points around it to create a new control point. Unfortunately this will lose some data given in the medial axis possibly making a high resolution medial axis as accurate as a medium resolution data set. Averaging out the control points also encounters the same problem as increasing the order of a curve which is that it can still make a control point go outside the vessel. However, unlike increasing the order of a curve, when averaging the points, one can take into account the radius of the medial axis and make sure the control point is staying inside the vessel. The last reason of versatility was the main reason for choosing to change the control points rather than increasing the order.

    Before we could begin experimenting with our smoothing algorithm we first had to create an environment where we could quickly and easily ascertain how well it smoothed out the curve and how well it stayed within the bounds of the vessel. AVS was not a good environment because it takes a night to render a movie and a 3D environment is not a simple enough place to experiment. Instead we used a separate DOS program which we also used for experimenting with other curves. To create the experimental environment we first randomly created a 2D tube used to represent a vessel. The tube varied in radius and progressed from left to right. To create a medial axis similar to the one given to us we created a medial axis made up of points inside the tube, but randomly displaced on the Y axis. From here we ran our smoothing procedure on the fake medial axis and determined if it was any good by looking at the generated image.

    The final procedure used was very simple and very effective. We ran through each point and output the average of that point and the point before and after it into another array. We also kept the same starting point and ending point. This new array was then made as the new control points in the curve. Running this algorithm once smooths out the curve somewhat, but not enough so to create a smooth animation. If  we ran our algorithm four times, we got a much smoother curve. We also changed the matrix from a B-spline to a Catmull-Rom so we could control where the curve went better and by using the Catmull-Rom curve we know that the curve will go through all the control points that we give it.

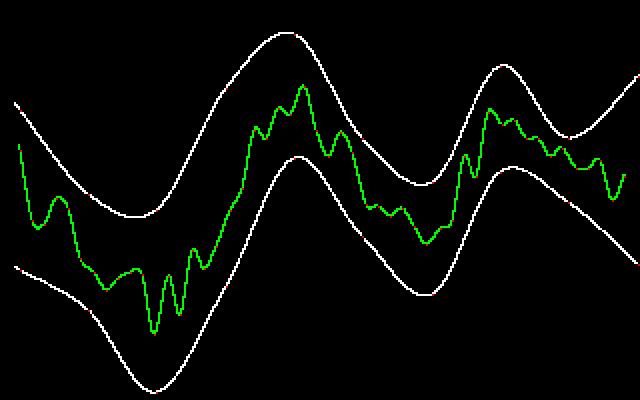
    This first picture shows our representation of a given medial axis. As the medial axis given to us, it is within the bounds of the vessel, has many points, and moves around a lot compared to the vessel.

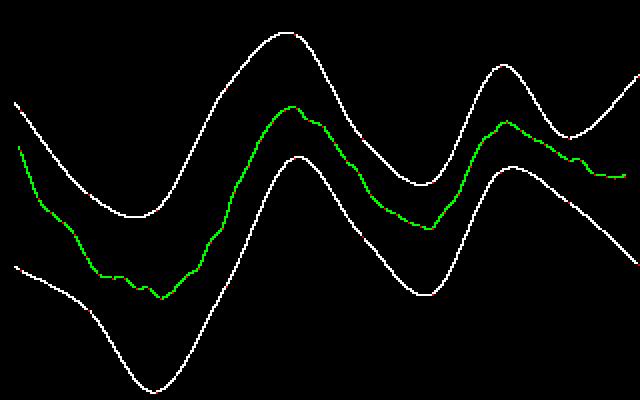
    The next picture shows our medial axis after running the smoothing algorithm on it twice.

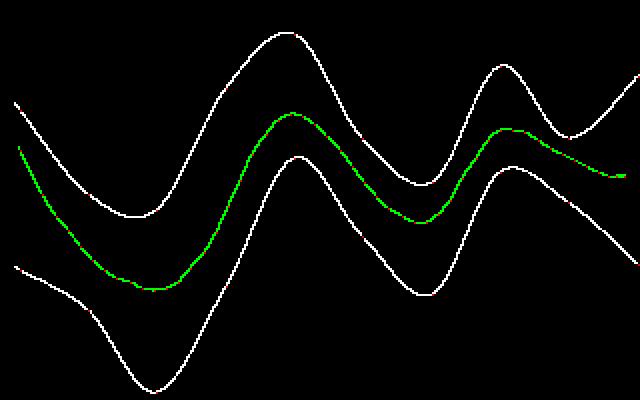
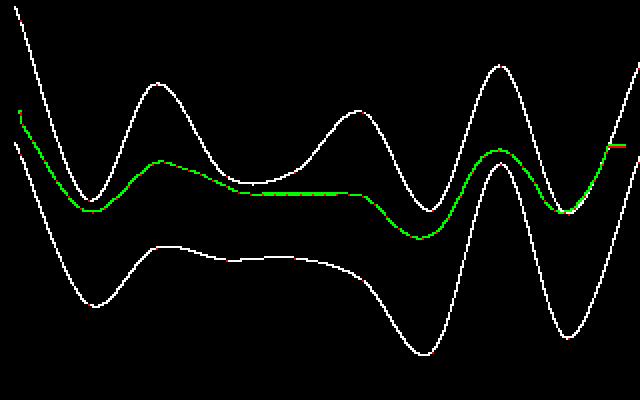
    As shown above, smoothing the curve out too much will result in a medial axis that breaks the bounds of the vessel, so it is necessary to smooth the correct amount.