[Table of Contents] [Next]
 

Basic Steps of the Finite Element Method

As stated in the introduction, the finite element method is a numerical procedure for obtaining solutions to boundary-value problems. The principle of the method is to replace an entire continuous domain by a number of subdomains in which the unknown function is represented by simple interpolation functions with unknown coefficients. Thus, the original boundary-value problem with an infinit number of degrees of freedom is converted into a problem with a finite number of degrees of freedom, or in other words, the solution of the whole system is approximated by a finite number of unknown coefficients.  Therefore, a finite element analysis of a boundary-value problem should include the following basic steps:
  1. Discretization or subdivision of the domain
  2. Selection of the interpolation functions (to provide an approximation of the unknown solution within an element)
  3. Formulation of the system of equations ( also the major step in FEM. The typical Ritz variational and Galerkin methods can be used.)
  4. Solution of the system of equations  (Once we have solved the system of equations, we can then compute the desired parameters and display the result in form of curves, plots, or color pictures, which are more meaningful and interpretable.)
The first step and the last step are most relevant with the visualization process. These 2 steps are described in greater detail below.

Domain Discretization

The discretization of the domain is the first and perhaps the most important step in any finite element analysis because the manner in which the domain is discretized will affect the computer storage requirements, the computation time, and the accuracy of the numerical results. The subdomains are usually referred to as the elements.

For a 1D domain which is actually a straight of curved line, the elements are often short line segments interconnected to form the original line [Fig2(a)]. For a 2D domain, the elements are usually small triangles and rectangles [Fig2(b)]. The rectangular elements are, of course, best suited for discretizing rectangular regions, while the triangular ones can be used for irregular regions. In a 3D solution, the domain may be subdivided into tetrahedra, triangular prisms, or rectangular bricks[Fig2(c)], among which the tetrahedra are the simplest and best suited for arbitrary-volume domains.
 

 
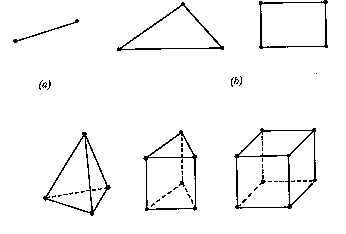 (c)
Figure2 Basic finite elements. (a) 1D (b) 2D (c) 3D

Note that the linear line segments, triangles, and tetrahedra are the basic one-, two-, and three-dimensional elements. Figure3 shows the finite element discretization of a 2- and 3- dimensional domain.
 

Figure 3 Examples of finite element discretization
(a) 2-D with triangular elements
   (b) 3-D with tetrahedra elements
The discretization of the domain is usually considered as a preprocessing task because it can be completely separated from the other steps. Many well-developed finite element program packages have the capability of subdividing an arbitrarily shaped line, surface, and volume into the corresponding elements and also provide the optimized global numbering.

Solution of the system of equations

Once we have solved the system of equations, we can then compute the desired parameters and display the result in form of curves, plots, or color pictures, which are more meaningful and interpretable. This final stage, often referred to as post-processing, can also be separated completely from the other steps.

Index | Next