Touring in N-Land

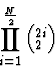
The touring mechanism in N-Land can be best likened to the channel controls on a television. Two controls are provided; one for selecting the pairings of the dimensions and one to set the speed of each pairing. A tour of the mappings produced by this technique would include all possible pair-wise combinations of the dimensions viewed at all permutations of speeds. By using two controls the user can easily step through the dimensional channels, with each one allowing a new picture (mapping of the data) to be viewed. If the assumption is made that the human brain is equally capable of interpreting patterns arranged horizontally or vertically, the orientation is less important than the actual pairings and speeds. Unique numbers are assigned to each channel to allow easy selection of ``favorite'' channels, to permit rapid sequencing through the channels, and to keep track of previously examined significant views.

One thing to consider is that, like any ``Grand Tour'' progression through a data set, the number of possible distinct mappings increases dramatically as the number of dimensions increases. For the case of taking the dimensions in unordered pairs, the number of possible orthogonal mappings for an N-dimensional data set is computed by

$$\prod_{i = 1}^{\frac{N}{2}} \left(^{2i}_{2} \right)$$

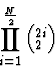
Although this number can get quite large (see Table 1), since only orthogonal mappings are being considered it is a more reasonable number to scan through than the methods that require the examination of all possible views. Once the ``rough'' orthogonal view is specified, finer adjustments can be made using the shearing mechanism, as described in the next section.

 

Table 1: How the number of orthogonal views changes with the number of dimensions.

Dimensions	Pairings	Orderings	Channels
2	1	1	1
4	3	2	6
6	15	6	90
8	105	24	2520
10	945	120	113400

An alternate method of selecting a view is what we term data-driven viewing (see Tipnis (19)). In this mode of operation, a user interactively selects a subset of points on the screen and instructs the system to find the view of the data which either maximizes or minimizes their spatial interrelationships on the screen. This is useful when the user suspects that certain points either represent distinct categories or share some relationship, and rather than flipping through the views in an attempt to verify this hypothesis, the user can permit the system to assist in this search.

In our current implementation of this process we employ the notion that differences in the slower dimensions are usually much more pronounced than those in the faster dimensions, as the slowest dimensions span the entire screen. Thus when we attempt to generate a view which causes the greatest clustering when mapped to 2-D, we want to have the dimensions for which there is the least variability in the selected subset of points to be used as the slow dimensions. Similarly, to maximize the dispersion of the data points on the screen, the dimensions with the greatest variability should be mapped to the slow dimensions. To perform this task, we compute the range of values for each dimension among the selected data points, compute the percentage of the full range of values this represents for each dimension, and sort these in ascending order. This provides the pairing and speeds for the dimensions to be used in the display.