Week 10

I. Matrix Representation of Networks

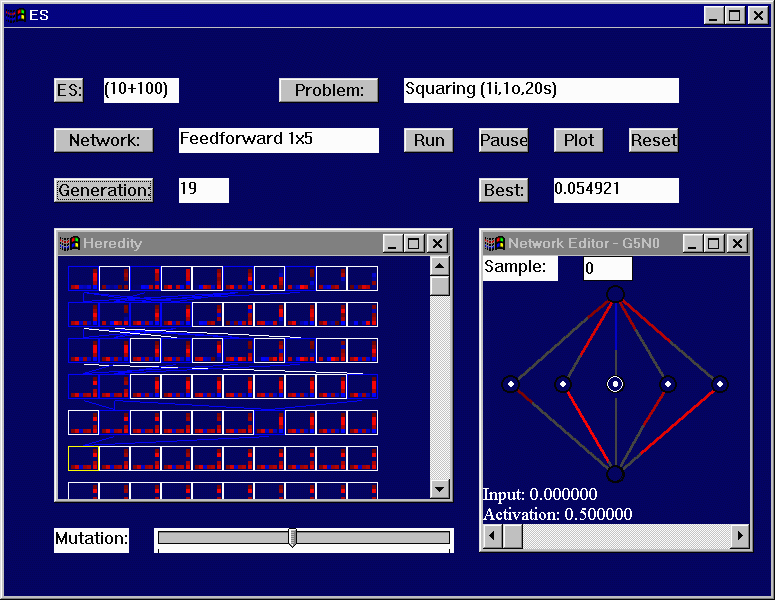
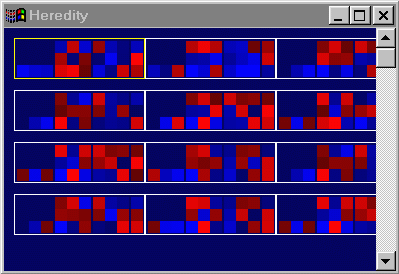
In our original discussion of compact weight representation, we were considering Hopfield networks, in which all nodes are interconnected, and therefore a single square matrix of color-coded pixels can represent the weights for a network. In representing feedforward networks, however, it is necessary to have a separate rectangular matrix for each layer. The "Heredity" window below illustrates this method. Each white box contains the matrix representation of a single network, and the highlighted (upper left) network is shown in its graphical form in the "Network Editor" window to the right.
Look inside the yellow box. The first row of three blue pixels represent the three weights coming out from the top node of the network, that is from the input layer to the first hidden layer. To the right of this is a 3x3 grid of pixels representing the weights going from the first hidden layer to the second. Row n, column m of this matrix represents the weight going from node n in the first hidden layer to node m in the second hidden layer. To the right of this is another 3x3 grid, representing the weights going from hidden layer 2 to hidden layer 3. The final column on the far right represents the three weights feeding into the output layer.
These rectangular matrices are organized such that, if you were to take the numerical weights associated with each pixel value and multiply the matrices left-to-right, you would obtain the transformation matrix that maps the input layer to the output layer (assuming linear activation functions).

II. Graphing Heredity

Six types of breeding can be used in Prof. Rana's code.
- In DISCRETE recombination, two random parents are selected, and each gene has a 50-50 chance of coming from either parent.
- In DISCMULT, each gene is taken from a randomly selected parent.
- In AVERAGED, two random parents are selected and each child gene is the average of the corresponding parent genes.
- For MEANMULT, a random parent is selected. For each gene, the child gene is assigned to the average of the corresponding gene in the parent and the corresponding gene in another randomly selected parent.
- WEIGHTED is like average, but uses a randomly weighted average.
- WGHTMULT is like MEANMULT, but uses a randomly weighted average.
For now I have confined my attention to the two-parent breeding types only, i.e. DISCRETE, AVERAGED, and WEIGHTED.
It is important to note that, when a new child is produced, separate breeding methods can be used for the weights and for the sigmas. Thus, in the cases I am dealing with, each child will have two weight-parents and two sigma-parents. Originally I simply intended to draw lines between all the children and their four parents. As shown below, this approach proved to be somewhat cluttered. Each row of networks represents the surviving members of a generation, ordered by fitness score, with the best networks on the far left.
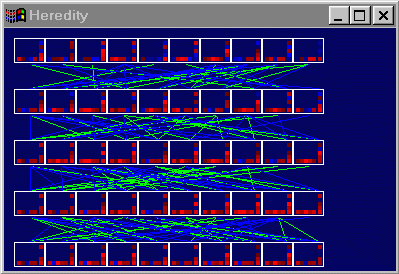
To remedy this crowding problem, I chose to display the parent links for the currently selected network only. I also chose to ignore sigma-parents for the moment, for the sake of simplicity. Finally, in the cases where a network actually survived from one generation to the next, a white link was drawn.