Weeks 12 & 13
I. Problems with Harder Problems
- I downloaded the complete set of training problems from the
Machine
Learning Repository at the University of California at Irvine, and
wrote a standalone program to convert the attribute-value samples to
numeric equivalents readable by my program.
- I tried two of what I thought were among the simpler problems in this
set, and unfortunately was not able to come anywhere close to convergence
on either. The problems I tried were tic-tac-toe (determining
whether the "X" or "O" player has three in a row), and balancing a scale
(given a weight and distance on the right and left, determine whether
the pivot point should be moved left or right to keep the scale from
tipping over).
- If the inputs to the balance-scale problem are i1,
i2, i3, and i4,
then, as we all know from physics, a network that solves this problem
simply needs to output:
- 1 if i1*i2 >
i3*i4
- .5 if i1*i2 =
i3*i4
- 0 otherwise
Since it seemed to me that the problems couldn't get much simpler than
this, I suspected there must be something wrong with my code. To test
this, I broke the balance-scale problem down into simple subproblems,
and attempted to design networks by hand that would solve them.
II. Designing Networks
- To make things easier on myself, I added a "File" menu to the Network
Editor that allows you to load and save networks. I then used a text
editor to design a network that would solve the comparison problem (i.e.
output a 1 if the first input is greater than the second, 0 otherwise).
By adding a "Network" menu with an "Eval" option, I was able to verify
that the comparison problem is solvable with my code.

- I was not, however, able to think of any way to design a network
to solve the multiplication problem. Clearly there must be a way for
neural networks to do this, but right now I cannot imagine what it is.
I wasn't able to evolve a network to solve this problem, either.
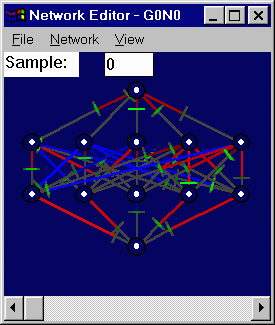
III. Visualizing Volatility
- In order to show the volatility (i.e. sigma magnitude) of each weight,
I drew a small line perpendicular to each weight. In keeping with the
scheme I used to show weight strengths, I drew a gray bar as a base, and
then drew a smaller green line on top of it, whose length and brightness
indicate the sigma strength.
- As the following two screen shots show, this approach works well
when the number of weights between layers is small, but gets crowded
fairly quickly as this value increases.
- In the screen shots above, the lengths of the green lines are scaled
linearly relative to the maximum sigma in the network. Originally, I
tried scaling relative the maximum possible sigma (i.e. the upper bound),
but this tended to produce a lot of very short lines which were
indistinguishable from each other.
IV. Executable Demo
- An executable demo of my ESWin program is available
here. This file contains ESWIN.EXE, as well
as some sample training sets and networks.