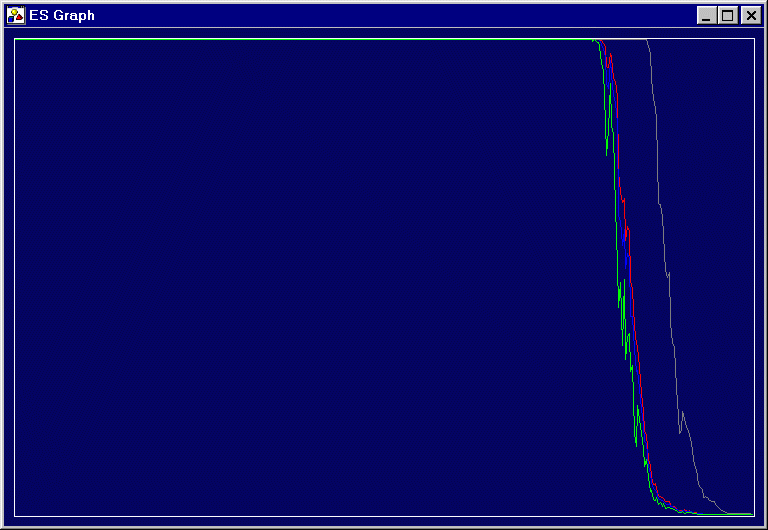
- The (mu,lambda) notation is used, where mu is the number of parents, lambda the number of children, and the best mu offspring are chosen as the next parent generation.
- The maximum (worst), minimum, and average fitness scores are graphed in red, green, and blue, respectively. Diversity is graphed in gray.
- The x-axis is the number of generations; the y-axis is the fitness or diversity value. Values are mapped onto the y-axis using a Sigmoid scale (the Sigmoid function maps all values from -inf to +inf onto the range 0 to 1). Thus the horizontal lines at the top of each graph are not "cutoffs"; the values are simply so large that their Sigmoid function, when rounded to the nearest pixel, ends up at the top.
ES: (10,100)
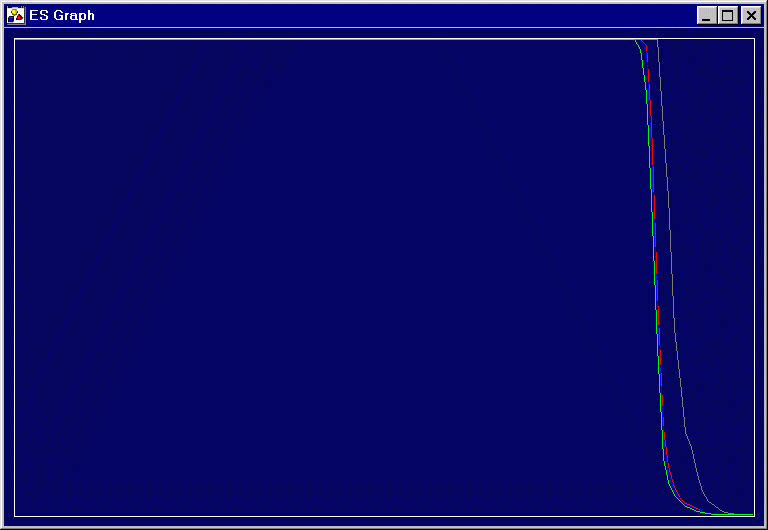
ES: (10,50)

ES: (5,100)