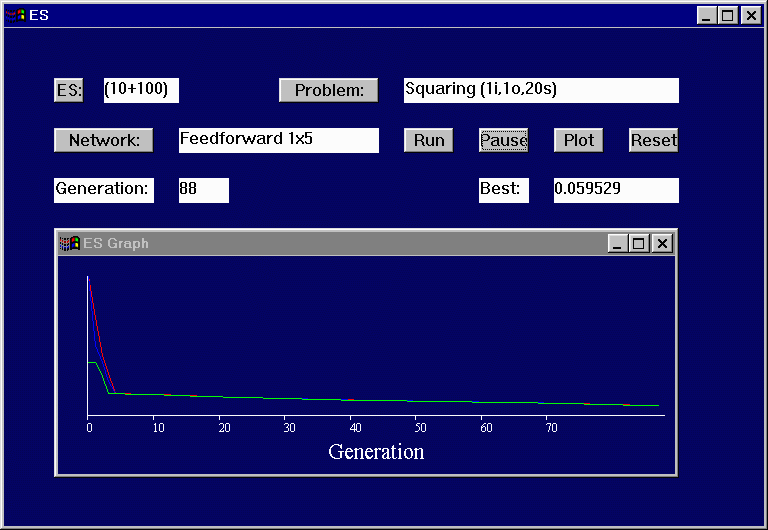
Figure 4.1: An early implementation of TESWindow.
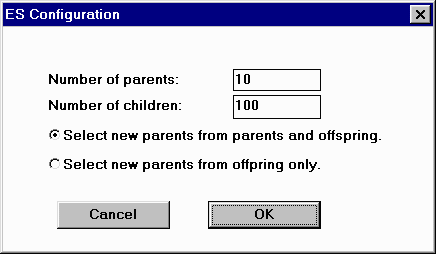
Figure 4.2: Evolution Strategies Configuration Dialog |
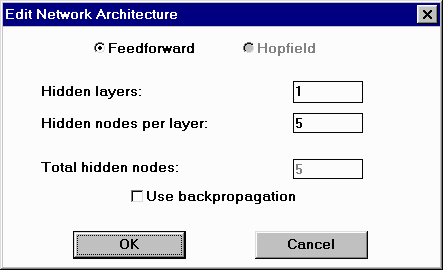
Figure 4.3: Network Architecture Dialog |
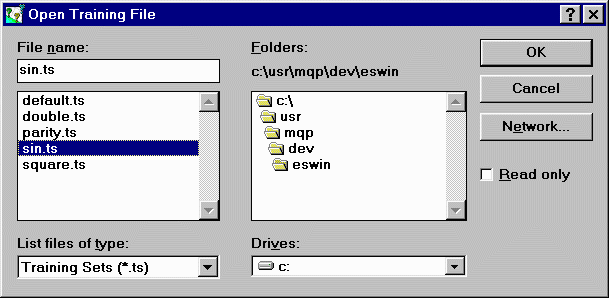
Figure 4.4: Load Training Set Dialog |
II. Implementation of TESGraphWindow

Figure 4.5: Original implementation of TESGraphWindow.
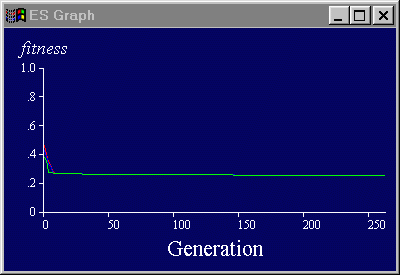 |
|
|
III. Implementation of TNVisWindow
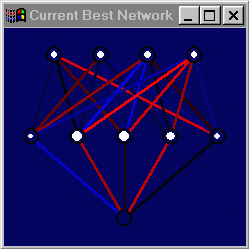 |
|
|
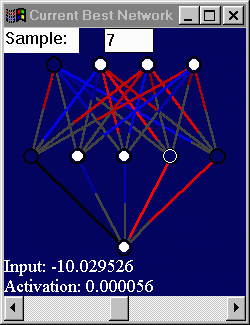 |
|
|
 |
|
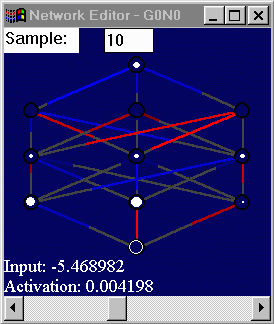
visualization of mutators associated with each weight. |
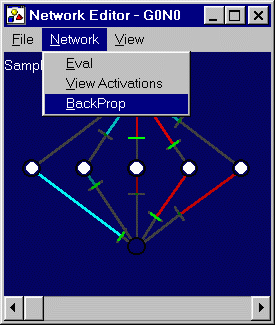
Figure 4.10: Final version of TNVisWindow. |
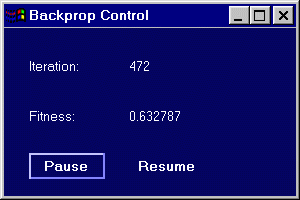
Figure 4.11: Associated Backprop Control window |
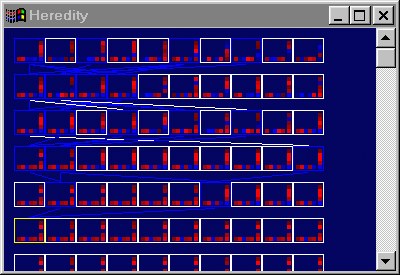
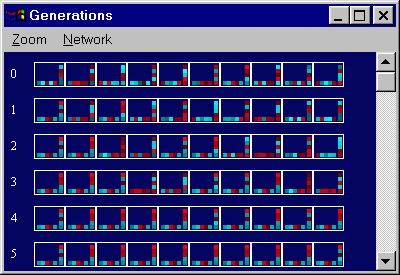
IV. Implementation of THeredityWindow & TGenerationWindow
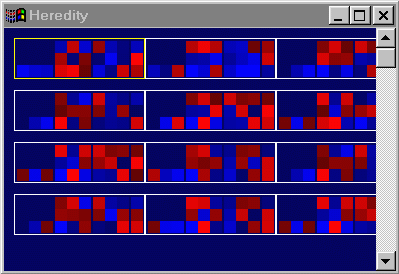 |
|
|
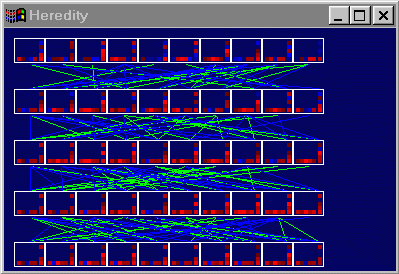
 |
|
left corner of Figure 4.12. |
 |
|
|
 |
 |
|
|
|
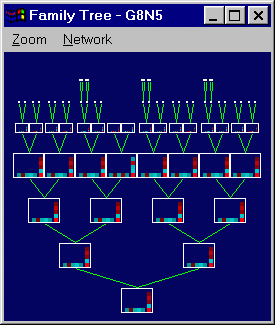
V. Implementation of TFamilyTreeWindow
 |
|
|
VI. Implementation of TESWindow

Figure 4.17: Final version of TESWindow.