|
Problem: Sine Wave
Description: The purpose of this problem was to output the sine of an angle given the angle as input. Training Set: 25 instances Test Set: 100 instances Network: 1 inputs; 2 hidden layers of 5 nodes each; 1 output. Sigmoid activation functions for hidden layers; linear activation functions for inputs and outputs. ES: (10+100) Generation: 1502 Training Fitness: 0.024021 Test Fitness: 0.024522 Comments: Problem solved to within reasonable accuracy. |
|
|
Problem: Squaring
Description: The purpose of this problem was to output the square of a number between 0 and 1 given the number as input. Training Set: 20 instances. Test Set: 100 instances. Network: 1 input; 2 hidden layers of 5 nodes each; 1 output. Sigmoid activation functions for hidden layers; linear activation functions for inputs and outputs. ES: (10+100) Generation: 501 Training Fitness: 0.004636 Test Fitness: 0.005306 Comments: Problem solved to within reasonable accuracy. |
|
|
Problem: 4 Bit Parity
Description: The goal of this problem was to determine the parity (odd or even) of a four bit word, represented as four distinct boolean-valued inputs. The network is expected to produce an output of 1 for a word with odd parity, 0 otherwise. Training Set: 16 instances (all possible combinations). Test Set: Identical to training set. Network: 4 inputs; 1 hidden layer of 5 nodes; 1 output. Sigmoid activation functions used for all layers. ES: (10+100) Generation: 3039 Training Fitness: 0.000000 Test Fitness: 0.000000 Comments: Problem solved. |

|
|
Problem: Balance Scale (Siegler76)
Description: This problem involved determining in which direction a pivot should be moved to balance a scale. Inputs to the problem were the two weights on the left and right side of the scale, and the distances of the two weights from the pivot. Possible outputs were move-to-left, move-to-right, and stay-in-place. Training Set: 30 instances Test Set: 605 instances Network: 4 inputs; 1 hidden layer of 10 nodes; 1 hidden layer of 1 node; 1 output. Sigmoid activation functions for hidden layers; linear activation functions for inputs and outputs. ES: (10+100) Generation: 1000 Training Fitness: 0.008932 Test Fitness: 0.170015 Comments: Training fitness is excellent; test fitness is mediocre. Test fitness is < 1/4, so that at least 50% of the test samples will be solved correctly. |
|
|
Problem: Balloon Classification
Description: This highly fictional problem consisted of the classification of a set of balloons according to a simple rule: a balloon is inflated if its color is yellow and its size is small. The balloon is deflated otherwise. Training Set: 20 instances Test Set: Identical to training set Network: 4 inputs; 2 hidden layers of 2 nodes each; 1 output. Sigmoid activation functions for hidden layers; linear activation functions for inputs and outputs. ES: (10+100) Generation: 256 Training Fitness: 0.000261 Test Fitness: 0.000261 Comments: Problem solved. |

|
|
Problem: Predict Housing Value
Description: The purpose of this problem was to predict the average retail value of houses in a development given 13 attributes, including average number of rooms, accessibility to highways, and property tax rates. The data were drawn from actual Boston-area housing developments (Harrison78). Training Set: 200 instances Test Set: 506 instances Network: 13 inputs; 1 hidden layer of 4 nodes; 1 hidden layer of 2 nodes; 1 output. Sigmoid activation functions for hidden layers; linear activation functions for inputs and outputs. ES: (10+100) Generation: 6488 Training Fitness: 0.061495 Test Fitness: 0.089019 Comments: The given network well on both the training and test sets. The fitness scores corresponds to predicting the average retail price to within about $3000 and $4500, respectively. |
|
|
Problem: Predict CPU Performance
Description: The goal of this problem was to predict the "relative performance" of a CPU given six attributes, including cache size, MHz rating, and main memory size. The expected output is a relative performance rating, originally specified on a scale of 0 to 1000 but normalized for our purposes into the range 0 to 1. Training Set: 60 instances Test Set: 209 instances Network: 6 inputs; 1 hidden layers of 3 nodes; 1 hidden layer of 1 node; 1 output. Sigmoid activation functions for hidden layers; linear activation functions for inputs and outputs. ES: (10+100) Generation: 244 Training Fitness: 0.019399 Test Fitness: 0.047041 Comments: Problem solved to within reasonable accuracy. The given network predicts the performance of the CPUs in the training set to within about 2%, and within under 5% in the test set. |
|
|
Problem: Image Recognition
Description: This problem involved the classification of images into one of seven classes: brickface, sky, foliage, cement, window, path, or grass. The image was presented to the network as a set of 19 inputs, each of which represented some aspect of the image. Inputs included the x and y coordinates of the image centroid, the mean pixel intensity, measures of contrast, and other characteristics. Training Set: 60 instances Test Set: 210 instances Network: 19 inputs; 1 hidden layer of 10 nodes; 7 outputs. Sigmoid activation functions for hidden layers; linear activation functions for inputs and outputs. ES: (10+100) Generation: 532 Training Fitness: 90.0% Test Fitness: 71.0% Comments: The network performs reasonably well, though far from perfect, on both the training and test sets. A special evaluation function was created for this problem and used as the fitness score in the ES algorithm. Each of the seven outputs in this network corresponds to one of the seven image classes mentioned above. For each sample, the maximum output produced by the network is taken to be the image class into which the network predicts the sample image will fall. This is compared with the actual image class for each sample, and the fraction of correct guesses is computed as the fitness score. |
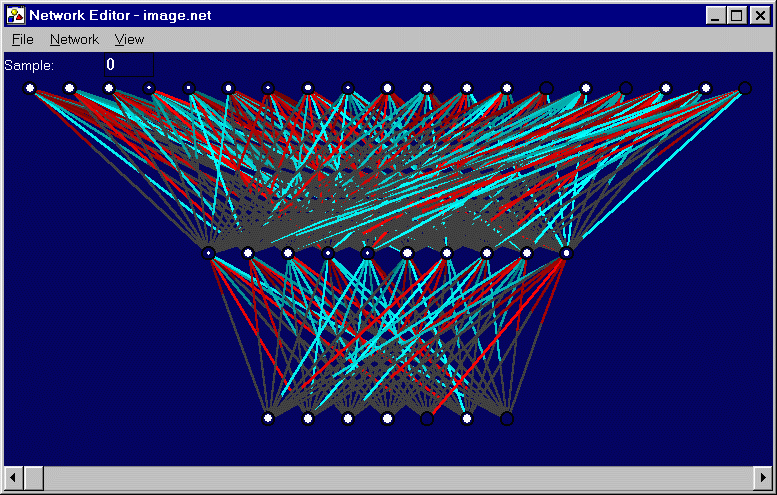
Figure 5.8: Network trained to solve the Image Recognition problem.
|
Problem: Breast Cancer Diagnosis (Wolberg90)
Description: This problem involved the diagnosis of lumps as malignant or benign based on a number of attributes, including proportion of normal nucleoli, epithelial cell size, and mitoses. Training Set: 200 instances. Test Set: 699 instances. Network: 9 inputs; 2 hidden layers of 2 nodes each; 1 output. Sigmoid activation functions for hidden layers; linear activation functions for inputs and outputs. ES: (10+100) Generation: 299 Training Fitness: 0.099739 (96%) Test Fitness: 0.101589 (95.6%) Comments: The network obtains significant convergence on both the training set and the test set. The RMS error is given, as well as the result of a special evaluation function which rounds the output of the network to the nearest available category (malignant or benign), and determines the fraction of instances that the network predicts correctly. Though the results of this special evaluation are given, the networks were trained using the standard RMS fitness score. An attempt was made to train the networks using the specialized evaluation function, but this did not produce better results. The percentages given here are comparable to those obtained by Wolberg using hyperplanes (Wolberg90), and by Zhang (Zhang92) using a variety of instance-based learning algorithms. |
|
II. Observations
A. A Voyage into Search Space
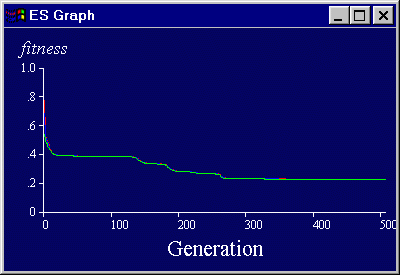
|
B. Understanding Genetic Drift
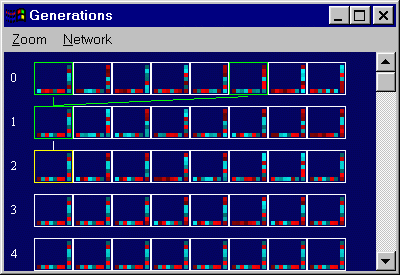
problem, generations 0 - 4. |
 |
 |
|
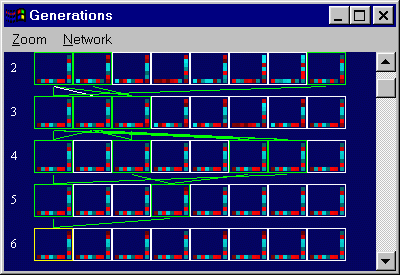
problem, generations 2 - 6. |
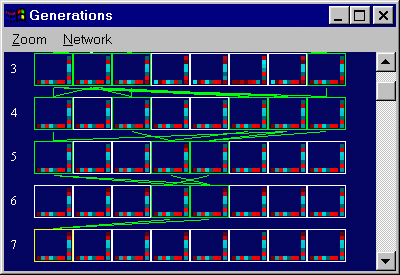
problem, generations 3 - 7. |
C. Changing Weights & Local Optima
III. The power of NVIS
A. Topological Optimization
B. Designing Networks
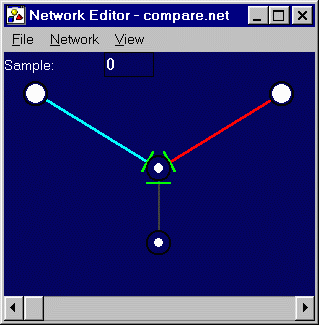
|
|
|
C. Extracting Domain Knowledge
|
||||||||||||||
|
|
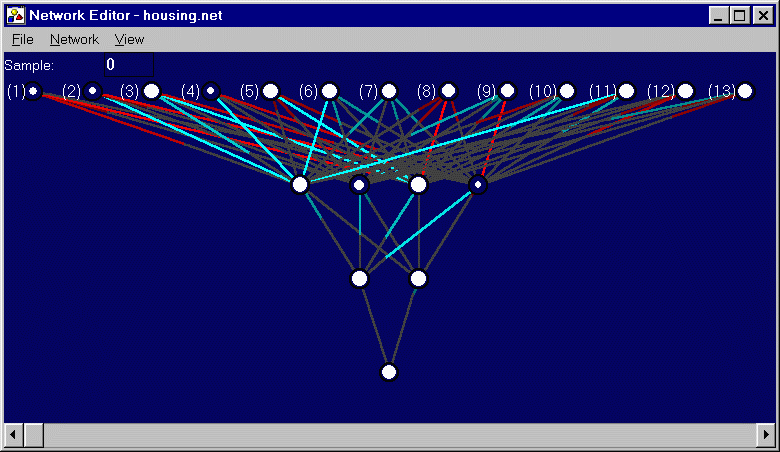
Figure 5.17: Network trained to solve Predict Housing Value problem, with input numbers overlaid on screen shot.