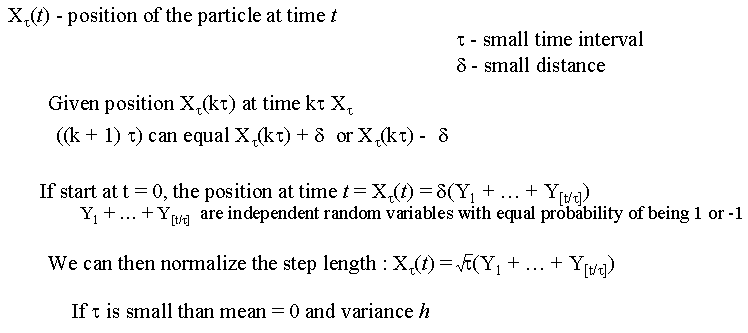
Fractional Brownian motion is also known as the "Random Walk Process." It basically consists of steps in a random direction and with a step-length that has some characteristic value. Hence the random walk process. A key feature to fBm is that if you zoom in on any part of the function you will produce a similar random walk in the zoomed in part. To get a good understanding of fBm we must first look at Brownian motion itself.

For any math buff out there, here is a methematical explaination of Brownian motion.

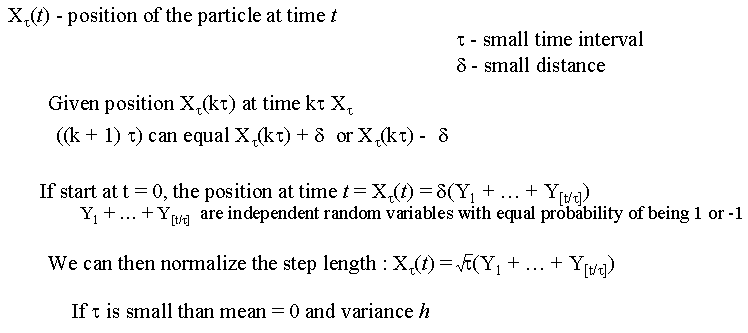
A slightly different definition:

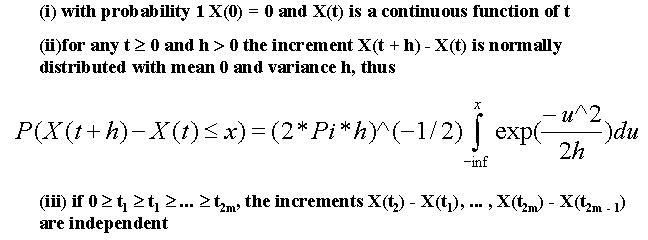
Some of you are probably sitting there trying to figure out just what these definitions mean. Put simply they mean that as you go along the function will either increment or decrement by a certain amount. This amount is determined by how close you are looking at the function. The integral in the second definition makes sure that as you get closer to the graph the amount the function changes gets smaller and smaller. In other words Brownian Motion is a line that will jump up and down a random amount and simular to the "How Long is the Coast of Britain?" problem, as you zoom in on the function you will discover similar patterns to the larger function.

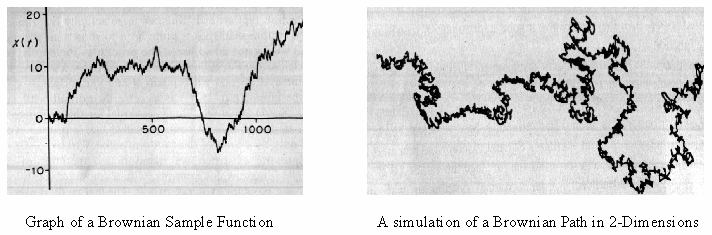
The two images above are examples of Brownian Motion. The first being a function over time. Where as t increases the function jumps up or down a varying degree. The second is the result of applying Brownian Motion to the xy-plane. You simply replace the values in the function with x and y. It gives you a nice random line that moves around the page.

As with before I will give you the mathematical description of the function:

The main difference between fBm and regular Brownian motion is that while the increments in Brownian Motion are independent they are dependent in fBm. This dependence means that if there is an increasing pattern in the previous "steps," then it is likely that the current step will be increasing as well.