An introduction to fractals

An Introduction to Fractals

Definition
Fractal Dimensions
Example: Calculate Fractal Dimension
How Long is the Coast of Britian?

According to Webster's Dictionary a fractal is defined as being "derived from the Latin fractus meaning broken, uneven: any of various extremely irregular curves or shape that repeat themselves at any scale on which they are examined."[0]

Mandelbrot, the discoverer of fractals gives two definitions:

"I coined fractal from the Latin adjective fractus. The corresponding Latin verb frangere means 'to break:' to create irregular fractments. It is therefore sensible - and how appropriate for our needs! - that, in addition to 'fragmented' (as in fraction or refraction), fractus should also mean 'irregular,' both meanins being preserved in fragment"[3]

Every set with a non-integer Hausdorff-Besicovitch dimension (D) is a fractal. However not every fractal has an integer D. A fractal is by definition a set for which D strictly exceeds the topological dimension (D^).[3]

Hausdorff-Besicovitch(Fractal Dimension)

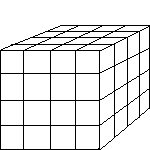
To understand the second definition we need to be able to uderstand the fractal dimension. So first we have to look at understanding how to calculate the dimension of an object. Below we have three different objects.

As you can see the line is broken into 4 smaller lines. Each of these lines is similar to the original line, but they are all 1/4 the scale. This is the idea of self similarity.

The square below is also broken into smaller pieces. Each of which is 1/4th the size of the original. In this case it takes 16 of the smaller pieces to create the original.

As with the others the cube is also broken down into smaller cubes of 1/4 the size of the original. It takes 64 of these smaller cubes to create the the original cube.

By looking at this we begin to see a pattern:

4 = 4^1

16 = 4^2

64 = 4^3

This gives us the equation:

N = S^D

Where N is the number of small pieces that go into the larger one, S is the scale to which the smaller pieces compare to the larger one and D is the dimension.

We now have the tools to be able to calculate the dimension. Just solve for D in the previous equation. When we do this we find that the Dimension is:

D = log N / log S

This dimension is the Hausdorff-Besicovitch dimension.

Example: Calculate Fractal Dimension

For an example of how to calculate the fractal dimension we are going to look at the Koch Curve. Here is the Koch Curve in action:

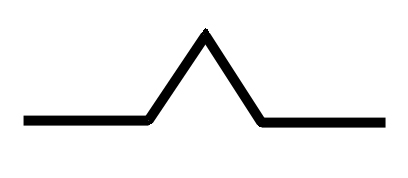
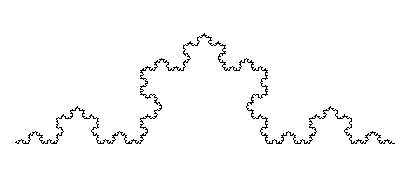
By looking at these pictures it is easy to see that a line in the Koch Curve breaks up into 4 smaller pieces. Each of these pieces are 1/3 the length of the original. Therefore N is equal to 4 and S is equal to 3. Which gives us a fractal dimension of 1.231... Since this is not an integer and it is greater than the topological dimention of 1, the Koch curve is therefore a fractal.

How Long is the Coast of Britain?

How long is the coast of Britain? This topic is a widely used method of explaining the use of fractals. How does one go about calculating the length of Britain? Reason would be to go out and measure it with some type of ruler. Does that give us an exact answer. The answer to that is no. A way to illustrate the reason behind this is below.

These pictures represent an imaginary coastline of Britain. The red lines are rulers being used to measure the length of the coastline (L). These rulers are of the length S. Using the first ruler we see that it L = 2 * S. When we decrease the length of S the number of times that S is used increases. What these rulers illustrate is that as the size of the measuring device becomes smaller the accuracy of the measurements become more and more accurate. From this fact you would assume that you would eventually be able to get an exact measurement of the coastline. This statement is false. As you decrease the size of the measuring device the length that you have to measure becomes greater. You can see this by zooming in on the coastline. As you get closer and closer you will notice that it looks very similar to how it looked from a greater distance away. Only now you are much closer. This observation show the self similarity of the coastline. Therefore as we decrease the size of the measuring device the length of the coastline will increase without limit. Thus, showing us its fractal nature.