It is a rather easy process to create rather realistic 2 dimensional islands using Brownian motion. To create an island you simply use a looping Brownian Motion function. A looping fuction is one that will eventually come back to its starting point after a finite number of steps. To create the 2D Brownian Motion function you simply replace X(t) with X(x,y). An example of an island created with this process is shown below.[3]

This image clearly shows the looping process of the Brownian function. To create the island you simply fill in the area that is enclosed within the loop created by the function. The result is a very nice looking islnd. An example showing the filled in island without the lines is displayed below.

As with Brownian Motion it is a simple process to create a 3 dimensional island using fBm. To create an island using this method you simply replace t with (x,y). You can then thing of X(x,y) as the height of a surface at the point (x,y). When you do this for a plane with a given number of points you can create an island such as the one below. This island is the first island created by Mandelbrot using this method.[3]

While Brownian Motion and fBm are very good methods of creating realistic islands there is another method available to create them. This method is called mid-point displacement. The basic idea of this method is to take a point and then to displace it by a certain amount, and then take another point and repeat the process.

The image above illustrates the mid-point displacement method in 2 dimensions. You start out with two points. You then take the average of those two points to calculate the mid-point between the two. You then increase or decrease that point by a certain value. You then recursively repeat the process with more and more points. At each level of recursion the maximum amount that a point can change decreases. This decrease makes sure that the points flow together well and create a more realistic look. The speed at which the maximum change value decreases is controlled by a Roughness Function. This function is multiplied by the current maximum value to create a new maximum value. An example Roughness Function is:

To create mountains in 3 dimensions using this process you have to start out with some type of base. The three main types are illustrated below.

Triangle Base

• You start with a triangle and then break that triangle into four smaller triangles by calculating the mid-point between the three corners. You then raise or lower these new points by some value.
• Problems: Using a triangle for a base tends to cause a creasing effect. This effect is when unrealistic ridges called creases are created.

• Starting with a square base helps to lower the chances of having a creasing effect. You take a square and then break it down in to four smaller squares. The new points are then raised or lowered depending on a random value.
• Problems: There is a small chance of creasing.

• Using a hexigonal base completely prevent to creation of creases.
• Problems: It is a very complex process to break a hexigon into smaller hexagons.

The square diamond mid-point displacement method is one type of mid-point displacement using a square base. This method is illustrated below.

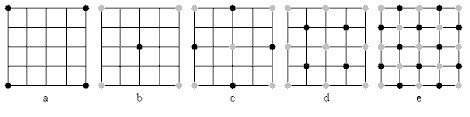
This methed uses a diamond style technique to calculate the mid-points. The first step in this method is to average all four corner points on the square. This averaging will give you the center point of the square. Next you displace that point by some amount. You then calculate the mid-points between the outer square by averaging all of the points surrounding that point. So if we wanted to calculate where the center top point in the square is, we would average the upper left corner with the upper right corner and the center point of the square. This process is then repeated using the smaller square. Using this method it is very easy to create tesselations out of the mountains. To do this you consider the point on any edge to be the exact same point as the point opposite from it. For example the upper middle point has the same value as lower middle point.

Here is some sample code that impliments the square diamond method.

Here are two examples of mid-point displacement at work:

• Wireframe Java Mountains
• Shaded Mountains with Details