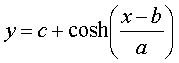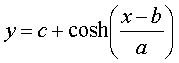Geometric Techniques

Geometric methods to model cloth are aimed at recreating the "look" of cloth and not its properties. This method is mainly employed by computer graphic people who are only trying to create images of the cloth that look realistic enough to be believed, but don't need the cloth to have the exact characteristics of cloth.

Weil
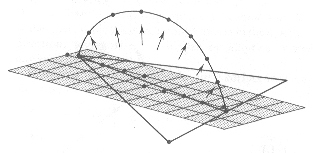
Weil was one of the first people to attempt to simulate cloth. His technique is the basis for almost all other techniques that have been developed since. The method that he created was to represent hanging cloth as a grid or points. He simulated its shape by fitting catenary curves between hanging restraint points. His method can be broken down into a two stage process. The first stage is to approximate a solution to the shape of the cloth and the second state is to apply certain restraints to the first stage to get a more realistic look.

The first step of the first stage is to set the cloth onto a square grid. This grid will be a representation of the cloth. The second step is to pick a triangle and hang a catenary curve from one of its corners to the midpoint of the other side of the triangle. Weil uses this equation for the catenary:

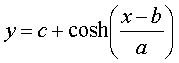
The next step is to move all of the points that lie on the line created by the catenary to the catenary curve. A rasterized line is drawn between the two end points of the catenary curve. The number of points that make up this line are counted and uniformly divide the catenary by this number. The points are then moved onto their corresponding location on the catenary.

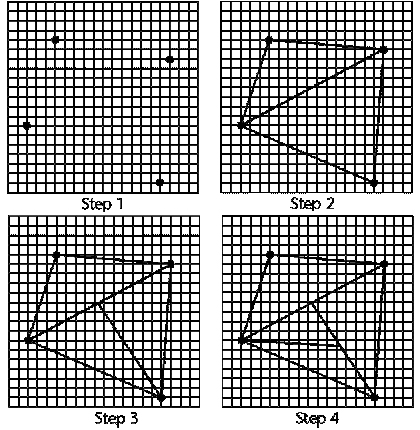
If there are still points that are not lying on the catenary withing the two triangles created by the splitting of the original triangle with the catenary, then the above process is repeated on these new triangles. The process is repeated on every triangle until all points are represented by a catenary. This splitting process can be seen below.

One problem with the steps discussed above is that there are more than one way to split a triangle with a catenary. To fix this problem a new catenary should be created that takes the original two into account. While this may solve the problem, it creates many calculations. Instead Weil decided to simply use the lower of the two catenaries. This solution solves the problem in a less computational way. The only problem with picking the lowest catenary is that during an animation the lower catenary may change from one frame to another creating a "snapping effect."

The second stage of the process is to apply restraints to the cloth shape to allow for a more realistic look. Weil did this through the use of a relaxation algorithm. During the first stage many of the points on the grid get moved into a location that would not be possible in a real cloth. The relaxation algorithm makes sure that the points are all located in relatively the same distance from each other as they were in their initial state.

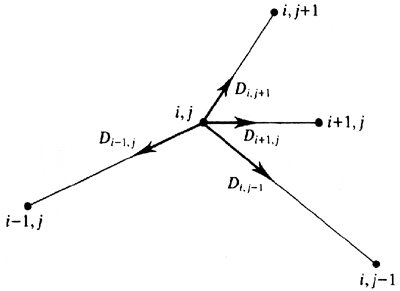
The first step in this process is to constuct displacement vectors between each point and its neighbors. The resultant displacement vector of the individual displacement vectors is then used to displace the point by some value to attempt to decrease the magniture of the overall displacement. This process is repeated over the whole grid until d_max (total displacement of the grid) is less than L (original distance to neighbors) + some tolerance factor. The displacement vectors are displayed below.

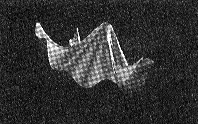
This method creates rather realistic looking cloth models. An example of this method can be seen below in the images of a ghostly shaped cloth model.

Agui et al
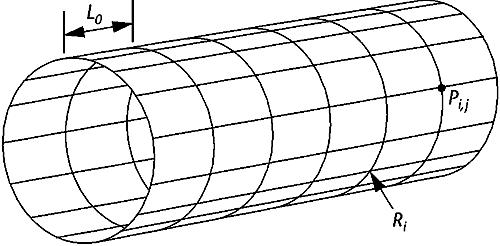
Agui and his colleges create a method to model cloth on a bending arm. They represented cloth as a hollow cylinder consisting of a series of circular rings. The image below is of the representation that they used.

Agui et al observed that folds formed as a direct consequence of the difference in curvature between the intter and out part of a bent sleeve. They were able to derive the following equation from this observation.

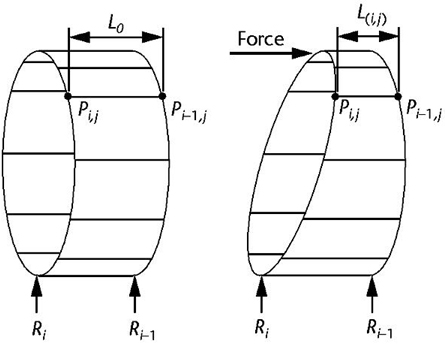
L(i,j) is the distance between the points P_i,j and P_i-1,j. dL(i,j) is the difference in distance before and after a bend. They determined that a deformation (fold) occurs when dL(i,j) is at a minimum. A before an after image of a bending is shown below.

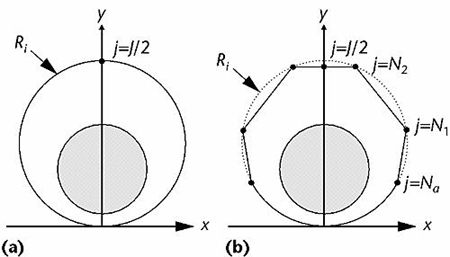
Folds are created by transforming the circular rings into polygons. The image below whow the circle R_i on the xy-plane before and after it is split into polygons. The shaded circle inside or R_I is the representations of the arm. To make the computations simple the circles are assumed to by symmetric about the y-axis. The first step in turning the rings into polygons is to find a point N_a where dL(i,j) is greater than some predetermined threshold dL_a. The parts of the circle below the point N_a are not changed and remain in circular form. The next step is to locate points N_1 and N_2 with thresholds dL_1 and dL_2 where dL_2 > dL_1 > dL_a. The algorithm that they used always assigns the top of the sleep to be flat. This is based on the assumption that folds are always flat near the top of the sleeve. This process is applied to all circles that makeup the sleeve. the corners are smoothed smoothed and averaged before rendering.