Dynamical Behavior of Hair
One-Dimension Projection
Physics Approximations (Inertia Moment)
Once we have created a reliable model of hair we must then be able to recreate the hair
dynamics, such as blowing in the wind, swaying from walking or running, etc. To model these
dynamics we must consider the hair to be composed of segments made of rigid sticks. This
assumption allows us to solve one dimensional differential equations of angular momentum. This
assumption also simplifies collision and interaction.
One-Dimension Projection
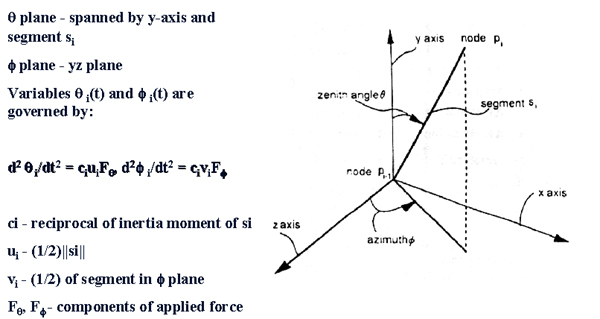
The first thing we want to consider is the dynamics of a single hair. To do this we use the
coordinate system show above. The behavior of bothe the zenith andgle and the azimuth angle of the
i-th segment of the hair are observed in this system. More importantly, consideration is given to
the shadow of the segment in the theta and phi planes. The theta plane is defined as the plane
spanned by the y-axis and the segment. If the segment is almost parallel to the y-axis, then the
theta plane is defined using the y-axis and some applied force instead of the segment. The phi plane
is defined as the zx-plane. The two equations for theta(t) and phi(t) are defined as show above.
These equations govern the animation of the segment.
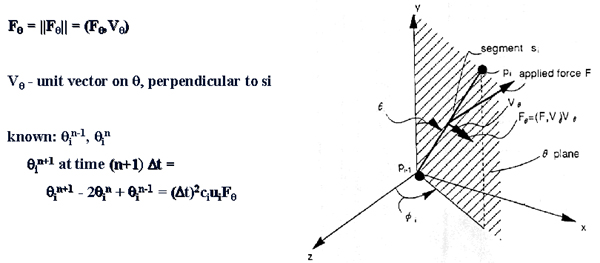
The component of the force in the theta plane is the scalar value that is defined as F_theta =
||F_theta|| = (F, V_theta). V_theta is the unit vector on the theta plane that is perpendicular
to the segment. If we know the current angle theta of the segment and the previous value of theta then
we are able to calculate the next value of theta using the equation show above. Theta_n+1 =
(delta t)^2 * c_i * u_i * F_theta.
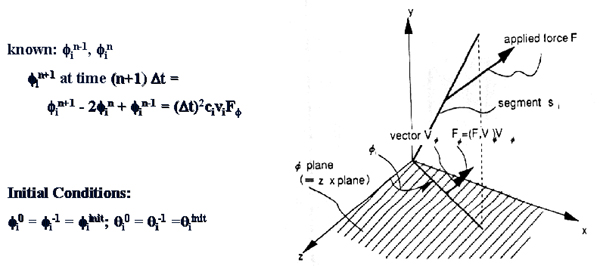
The component of the force in the phi plane is the scalar value that is defined as F_phi = ||F_phi|| =
(F, V_phi), where V_phi is the unit vector on the phi plane that is perpendicular to the hair segment.
As in the theta plane we are able to come up with a formula to calculate the new value of phi. This
equation is shown above.
Now that we have these equations to animate our hair model, we must set up some initial conditions. One
example is to set Phi_0 = Phi_-1 = Phi_init and Theta_0 = Theta_-1 = Theta_init. This means that the
hair is at it initial state and has not gone through any type of animation.
Physics Approximations (Inertia Moment)
When we model the dynamic behavior of hair we also have to take into account some physical properties, such
as the inertia moment of the hair. To approximate this property lets consider a stick S with a
length kd, with a density of rho. It inertia moment can then be calculated with I_S = (1/3) * rho * (kd)^2.
This equation if very closely related to the c_i * v_i and c_i * u_i in the plane projections discussed above.
If we suppose that the inertia moment I_s of the segment s_i is proportional to 1/i and that I_k is equal
to I_S, then I_i is given as I_i = (rho / 3*i) * k^3 * d^2. Also the term (delta t)^2 * c_i * u_i can
be represented as {3 * (delta t)^2 * i} / (2 * k^3 * rho * d).
The self-interaction off the hair can be described by arranging c_i values. For example if the c_i's are small
for the segments near the top of the head, tthen the hair near the top moves relatively slowly. In otherwords
c_i represents the hair's friction coefficient.

Here is an example of a simulation of a wind gust. We set the initial conditions to be: t = 0.1,
d = rho = 1.0, k = 1, where k is the maximum number of segments allowed to compose a piece of hair. The
model shown above was created with 10,000 individual hairs. Frame 0 shows the initial state of the system.
In frame 1 through 15 the force being applied to the hair is F = (-200, 0, 0). As you can see the hair starts
to blow back, but due to the inertial moment not all of the hair moves back at the same rate. You can see
that the hair in the back blows backwards faster than the hair on the top of the head. At frame 16 the force
is changed to F = (-20, -250, 0). This change in the force is to simulate the turbulent nature of wind. As you can
see from the image of frame 20 that some of the hair still moved in the original direction due to inertia.
Another physical property that we had to recreate was to keep the hair from colliding with the head during an
animation. This problem was dealt with through the use of a pseudo-force field. The variables required for
this calculation are displayed below.

What the pseudo-force field does is limits the effect that the force has on the hair the closer the hair
is to the head model. If the hair segment is located close to the head model than the force being appplied
to that segment will be quickly reduced to 0. This method easily iliminates collisions between the hair and
the head model.

Shown above are examples of using the pseudo-force field. The top images is showing the initial state where there is
no force being applied to the image. The bottom-left image shows what happens when the pseudo-force field does not limit
the movement of the hair. As you can see from this image, it is not very realistic. The hair on the right
side of the head go through the head model. Real hair will not do this. Now, the final image shows what happens
when the movement of the hair is limited by the pseudo-force field. The hair that had previously gone through
the head model now do not. This is much more realistic and gives a good effect.
One last physical property that we will look at is the stiffness of the hair. The equations to simulate stiffness in
hair are displayed below.

As you can see this is a relatively simple process. If the angle between two hair segments is greater
than the given stiffness angle, then that angle is lowered to the stiffness angle. That's it! There aren't
any complicated formulas or computations needed. An example of this method is shown below, where some
hair segments are set to be stiffer than others. The effect is easy to see.