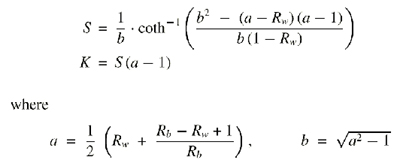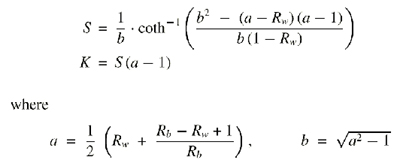Rendering the Pigmented Layers
Specifying the Optical Properties of Pigments
Optical Compositing of Layers
Pigment Examples
Kubelka-Munk Model
In developing a method to render the pigmented layers we used the Kubelka Munk model to
perform the optical compositing of the glzed layers. In our model each pigment is assigned
a set of absorption coefficients K and scattering coefficients S. The coefficients control the
fraction of energy that is absorbed and scattered back per unit distance in a layer of pigment.
We composed K and S out of three coefficients to represent the their RGB components.
Specifying the Optical Properties of pigments
Normall the K and S values for any given colorant layer are determined experimentally using
spectral measurements from layers of know thicknesses. To simplify this process we allow the
user to specify coefficients intercactively by choosing the desired appearance of a unti thickness of
the pigment over both a white and black background. We are then able to calculate the K and S value
for the pigment using the following formula.
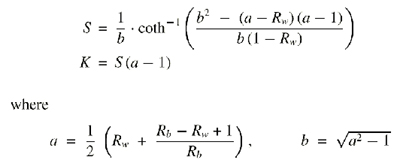
In order to prevent division by 0 we requre that 0 < R_b < R_w < 1 for each color channel. This
requirement causes most K an S values to fall in the legal range of 0 to 1. For certain very saturated
input colors the absorption or scattering coeeficients may exceed 1. We have not found this to be
a problem and our method will still work with these colors.
Opaque Paints
Opaque paints exhibit a similar color on both a whit and black background. This property is caused by a high
scattering in the same wavelengths as their color and high absorption in complementary wavelengths.
Transparetn Paints
Transparent paints appear colored on a white background and nearly block on a black background. This property is
caused by a low scattering in all wavelengths and high absorption in wavelengths complementary to their color.
Interference Paints
Interference paints appear white on a white background and colored on a black background. This property is
caused by a high scattering in the same wavelengths as their color and low absorption in all wavelengths.
Optical Compositing of Layers
Given scattering and absorptioin S and K for a pigmented layer of a given thicknexx x, we are able to
compute the reflectance R and tranmittance T with the following equations:
R = sinh(bSx/c)
T = b/c
where c = a sinh(bSx) + b cosh(bSx)
We are then able to compute the overall reflectance and transmittance of two abbutting layers with
the following equations:
R = R_1 + T^2_1 * R_2 / (1 - R_1 * R_2)
T = T_1 * T_2 / (1 - R_1 * R_2)
By repeationg these equations for each additional glaze we are able to calculate the overall reflectance
R to render the pixel.
For individual layers containing less than 1 pigment of thichnesses x^1, ..., x^n S and K of
each pigment are weighted in proportion to that pigments relative thickness.
Pigment Examples

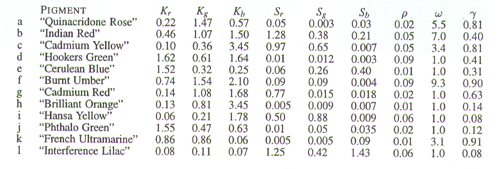
The images above display the palette of colors used in our examples, with each pigment
shown as a swatch painted over a black stripe. The K and S coefficients for these colors are displayed
below them.
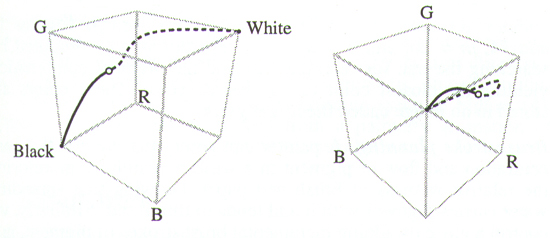
The image above shows the range of colors, in a 3D space, obtainable by glazing "Hansa Yellow" over both white and
black backgrounds. As you can see there is a difference in the hue between the two curves. There is also a
difference in the level of saturation along each curve. This is one of the qualities that gives watercolor its
rich appearance.
Kubelka-Munk Model
The Kubleka-Munk model (KM) was designed for situations that are like watercolor, where there
are multiple pigmented layers that scatter and absorb light. In our use of the KM model we were
able to satisfy some assumptions and others only partially if at all. These points are discussed
below.
All colorant layers are immersed in mediums of the same refractive index
This assumption is violated at both the air to pigment layer and the pigment layer to paper boundaries.
The pigment particles are soriented randomly
This assumption is violated by matallic colors, which have mostly horizontal flakes.
The illumination is diffuse
The simulated watercolors that our method produces will not look right under all lighting conditions.
The KM equations apply only to one wavelength at time
This is violated by flourescent paints
There is no chemical or electrical interaction between pigments, or between the pigment
and medium, which would cause clumping grains and a non-uniform particle size
This assumption is violated by almos all watercolor pigments.
Although it may look like the KM model may be inappropriate for our simulation, we found that it
works pretty well.